
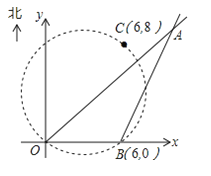
ΓΨΧβΡΩΓΩ‘ΎΡ≥’≈ΚΫΚΘΆΦ…œΘ§±ξΟςΝΥ»ΐΗωΙέ≤βΒψΒΡΉχ±ξΘ§»γΆΦΘ§OΘ®0Θ§0Θ©ΓΔBΘ®6Θ§0Θ©ΓΔCΘ®6Θ§8Θ©Θ§”…»ΐΗωΙέ≤βΒψ»ΖΕ®ΒΡ‘≤–Έ«χ”ρ «ΚΘ―σ…ζΈο±ΘΜΛ«χΘ°
Θ®1Θ©Ρ≥ ±ΩΧΚΘΟφ…œ≥ωœ÷“Μ”φ¥§AΘ§‘ΎΙέ≤βΒψO≤βΒΟAΈΜ”Ύ±±ΤΪΕΪ45ΓψΘ§Ά§ ±‘ΎΙέ≤βΒψB≤βΒΟAΈΜ”Ύ±±ΤΪΕΪ30ΓψΘ§«σΙέ≤βΒψBΒΫA¥§ΒΡΨύάκΘ°Θ®![]() Θ©
Θ©
Θ®2Θ©»τ”φ¥§A”…Θ®1Θ©÷–ΈΜ÷Οœρ’ΐΈςΖΫœρΚΫ––Θ§ «ΖώΜαΫχ»κΚΘ―σ…ζΈο±ΘΜΛ«χΘΩΆ®ΙΐΦΤΥψΜΊ¥πΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©16.2ΘΜΘ®2Θ©≤ΜΜα
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψAΉςADΓΆ![]() ÷α”ΎΒψDΘ§“άΧβ“βΘ§ΒΟΓœBAD=30ΓψΘ°‘ΎRtΓςABD÷–Θ§…ηBD=
÷α”ΎΒψDΘ§“άΧβ“βΘ§ΒΟΓœBAD=30ΓψΘ°‘ΎRtΓςABD÷–Θ§…ηBD=![]() Θ§‘ρAB=2
Θ§‘ρAB=2![]() Θ§”…Ι¥Ι…Ε®άμΒΟΘΚAD=
Θ§”…Ι¥Ι…Ε®άμΒΟΘΚAD= ![]() Θ§ΗυΨίΆΦ–ΈΒΟΒΫOD=OB+BD=6+xΘ§Ι AB=2x=6(
Θ§ΗυΨίΆΦ–ΈΒΟΒΫOD=OB+BD=6+xΘ§Ι AB=2x=6(![]() )Γ÷16.2
)Γ÷16.2
Θ®2Θ©ΙΐΒψAΉςAGΓΆy÷α”ΎΒψGΘ°ΙΐΒψOΓδΉςOΓδEΓΆOB”ΎΒψEΘ§≤Δ―”≥ΛEOΓδΫΜAG”ΎΒψFΘ°”…¥ΙΨΕΕ®άμΒΟΘ§OE=BE=3Θ°‘ΎRtΓςOOΓδE÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘ§OΓδE=4Θ°Υυ“‘OΓδF=5+3![]() >5.
>5.
Θ®1Θ©ΙΐΒψAΉςADΓΆ![]() ÷α”ΎΒψDΘ§“άΧβ“βΘ§ΒΟΓœBAD=30ΓψΘ°‘ΎRtΓςABD÷–Θ§…ηBD=
÷α”ΎΒψDΘ§“άΧβ“βΘ§ΒΟΓœBAD=30ΓψΘ°‘ΎRtΓςABD÷–Θ§…ηBD=![]() Θ§‘ρAB=2
Θ§‘ρAB=2![]() Θ§”…Ι¥Ι…Ε®άμΒΟΘΚAD=
Θ§”…Ι¥Ι…Ε®άμΒΟΘΚAD= ![]() Θ§”…Χβ“β÷ΣΘΚOD=OB+BD=6+
Θ§”…Χβ“β÷ΣΘΚOD=OB+BD=6+![]() Θ°‘ΎRtΓςAOD÷–Θ§OD=ADΘ§6+
Θ°‘ΎRtΓςAOD÷–Θ§OD=ADΘ§6+![]() =
=![]()
Γύ![]() =3Θ®
=3Θ®![]() +1Θ©Θ§
+1Θ©Θ§
ΓύAB=2![]() =6Θ®
=6Θ®![]() +1Θ©Γ÷16.2
+1Θ©Γ÷16.2
Φ¥ΘΚΙέ≤βΒψBΒΫA¥§ΒΡΨύάκΈΣ16.2Θ°
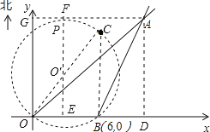
Θ®2Θ©Ν§Ϋ”CBΘ§COΘ§‘ρCBΓΈy÷αΘ§ΓύΓœCBO=90ΓψΘ§…ηOΓδΈΣ”…OΓΔBΓΔC»ΐΒψΥυ»ΖΕ®‘≤ΒΡ‘≤–ΡΘ°
‘ρOCΈΣΓ―OΓδΒΡ÷±ΨΕΘ°
”…“―÷ΣΒΟOB=6Θ§CB=8Θ§”…Ι¥Ι…Ε®άμΒΟOC=![]()
ΓύΑκΨΕOOΓδ=5
ΙΐΒψAΉςAGΓΆy÷α”ΎΒψGΘ°
ΙΐΒψOΓδΉςOΓδEΓΆOB”ΎΒψEΘ§≤Δ―”≥ΛEOΓδΫΜAG”ΎΒψFΘ°
”…¥ΙΨΕΕ®άμΒΟΘΚOE=BE=3Θ§Γύ‘ΎRtΓςOOΓδE÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚOΓδE=4
ΓΏΥΡ±Ώ–ΈFEDAΈΣΨΊ–ΈΘ§ΓύEF=DAΘ§ΕχAD=![]() =9+3
=9+3![]()
ΓύOΓδF=9+3![]() -4=5+3
-4=5+3![]()
ΓΏ5+3![]() ΘΨ5Θ§Φ¥OΓδFΘΨr
ΘΨ5Θ§Φ¥OΓδFΘΨr
Γύ÷±œΏAG”κΓ―OΓδœύάκΘ§A¥§≤ΜΜαΫχ»κΚΘ―σ…ζΈο±ΘΜΛ«χΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
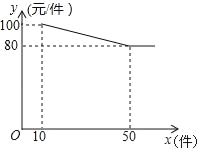
ΓΨΧβΡΩΓΩΖΰΉΑ≥ß≈ζΖΔΡ≥÷÷ΖΰΉΑΘ§ΟΩΦΰ≥…±ΨΈΣ65‘ΣΘ§ΙφΕ®≤ΜΒΆ”Ύ10ΦΰΩ…“‘≈ζΖΔΘ§Τδ≈ζΖΔΦέyΘ®‘Σ/ΦΰΘ©”κ≈ζΖΔ ΐΝΩxΘ®ΦΰΘ©Θ®xΈΣ’ΐ’ϊ ΐΘ©÷°ΦδΥυ¬ζΉψΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ°
Θ®1Θ©«σy”κx÷°ΦδΥυ¬ζΉψΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©…ηΖΰΉΑ≥ßΥυΜώάϊ»σΈΣwΘ®‘ΣΘ©Θ§»τ10ΓήxΓή50Θ®xΈΣ’ΐ’ϊ ΐΘ©Θ§«σ≈ζΖΔΗΟ÷÷ΖΰΉΑΕύ…ΌΦΰ ±Θ§ΖΰΉΑ≥ßΜώΒΟάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΈΜΆ§―ß5¥Έ ΐ―ß―ΓΑΈ»ϋΒΡ≥…Φ®Ά≥ΦΤ»γœ¬±μΘ§ΥϊΟ«5¥ΈΩΦ ‘ΒΡΉή≥…Φ®œύΆ§Θ§«κΆ§―ßΟ«Άξ≥…œ¬Ν–Έ ΧβΘΚ
ΒΎ1 ¥Έ | ΒΎ2 ¥Έ | ΒΎ 3¥Έ | ΒΎ 4¥Έ | ΒΎ5 ¥Έ | |
ΦΉ≥…Φ® | 90 | 40 | 70 | 40 | 60 |
““≥…Φ® | 70 | 50 | 70 |
| 70 |
Θ®1Θ©Ά≥ΦΤ±μ÷–Θ§«σ![]() ΒΡ÷ΒΘ§ΦΉΆ§―ß≥…Φ®ΒΡΦΪ≤νΈΣΕύ…ΌΘΜ
ΒΡ÷ΒΘ§ΦΉΆ§―ß≥…Φ®ΒΡΦΪ≤νΈΣΕύ…ΌΘΜ
Θ®2Θ©–Γ”±ΦΤΥψΝΥΦΉΆ§―ßΒΡ≥…Φ®ΤΫΨυ ΐΈΣ60Θ§ΖΫ≤ν «![]() [(90©¹60)2+(40©¹60)2+(70©¹60)2+(40©¹60)2+(60©¹60)2]ΘΫ360.
[(90©¹60)2+(40©¹60)2+(70©¹60)2+(40©¹60)2+(60©¹60)2]ΘΫ360.
«κΡψ«σ≥ω““Ά§―ß≥…Φ®ΒΡΤΫΨυ ΐΚΆΖΫ≤νΘΜ
Θ®3Θ©¥”ΤΫΨυ ΐΚΆΖΫ≤νΒΡΫ«Ε»Ζ÷ΈωΘ§ΦΉ““ΝΫΈΜΆ§―ßΥ≠ΒΡ≥…Φ®ΗϋΈ»Ε®.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
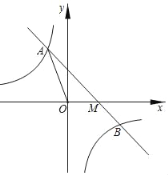
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ“Μ¥ΈΚ· ΐyΘΫ©¹x+2”κΖ¥±»άΐΚ· ΐyΘΫ![]() ”κΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§”κx÷αΫΜ”ΎΒψMΘ§«“ΒψAΒΡΚαΉχ±ξ «©¹2Θ§BΒψΒΡΚαΉχ±ξ «4Θ°
”κΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§”κx÷αΫΜ”ΎΒψMΘ§«“ΒψAΒΡΚαΉχ±ξ «©¹2Θ§BΒψΒΡΚαΉχ±ξ «4Θ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΓςAOMΒΡΟφΜΐΘΜ
Θ®3Θ©ΗυΨίΆΦœσ÷±Ϋ”–¥≥ωΖ¥±»άΐΚ· ΐ÷Β¥σ”Ύ“Μ¥ΈΚ· ΐ÷Β ±xΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΟΉ ÷Μζ‘Ϋά¥‘Ϋ ήΒΫ¥σ÷ΎΒΡœ≤Α°Θ§Ης÷÷Ων ΫœύΦΧΆΕΖ≈ –≥ΓΘ§Ρ≥ΒξΨ≠”ΣΒΡAΩν ÷Μζ»ΞΡξœζ έΉήΕνΈΣ50000‘ΣΘ§ΫώΡξΟΩ≤Ωœζ έΦέ±»»ΞΡξΫΒΒΆ400‘ΣΘ§»τ¬τ≥ωΒΡ ΐΝΩœύΆ§Θ§œζ έΉήΕνΫΪ±»»ΞΡξΦθ…Ό20%Θ°
Θ®1Θ©ΫώΡξAΩν ÷ΜζΟΩ≤Ω έΦέΕύ…Ό‘ΣΘΩ
Θ®2Θ©ΗΟΒξΦΤΜ°–¬Ϋχ“Μ≈ζAΩν ÷ΜζΚΆBΩν ÷ΜζΙ≤60≤ΩΘ§«“BΩν ÷ΜζΒΡΫχΜθ ΐΝΩ≤Μ≥§ΙΐAΩν ÷Μζ ΐΝΩΒΡΝΫ±ΕΘ§”Π»γΚΈΫχΜθ≤≈Ρή Ι’β≈ζ ÷ΜζΜώάϊΉνΕύΘΩAΘ§BΝΫΩν ÷ΜζΒΡΫχΜθΚΆœζ έΦέΗώ»γœ¬±μΘΚ
AΩν ÷Μζ | BΩν ÷Μζ | |
ΫχΜθΦέΗώΘ®‘ΣΘ© | 1100 | 1400 |
œζ έΦέΗώΘ®‘ΣΘ© | ΫώΡξΒΡœζ έΦέΗώ | 2000 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
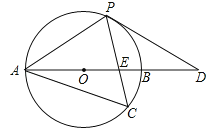
ΓΨΧβΡΩΓΩ»γΆΦΘ§“‘AB±ΏΈΣ÷±ΨΕΒΡΓ―OΨ≠ΙΐΒψPΘ§C «Γ―O…œ“ΜΒψΘ§Ν§ΫαPCΫΜAB”ΎΒψEΘ§«“ΓœACP=60ΓψΘ§PA=PDΘ°
Θ®1Θ© ‘≈–ΕœPD”κΓ―OΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©»τΒψC «ΜΓABΒΡ÷–ΒψΘ§“―÷ΣAB=4Θ§«σCECPΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫβ≤ΜΒ» ΫΉιΘ°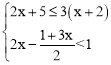 Α―≤ΜΒ» ΫΉιΒΡΫβΦ·‘Ύ ΐ÷α…œ±μ Ψ≥ωά¥Θ§≤Δ–¥≥ω≤ΜΒ» ΫΉιΒΡΖ«ΗΚ’ϊ ΐΫβΘ°
Α―≤ΜΒ» ΫΉιΒΡΫβΦ·‘Ύ ΐ÷α…œ±μ Ψ≥ωά¥Θ§≤Δ–¥≥ω≤ΜΒ» ΫΉιΒΡΖ«ΗΚ’ϊ ΐΫβΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
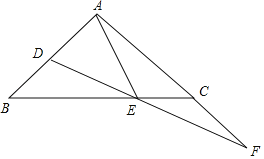
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§AB=ACΘ§ΓœBAC=90ΓψΘ§ΒψDΘ§EΖ÷±π‘ΎABΘ§BC…œΘ§ΓœEAD=ΓœEDAΘ§ΒψFΈΣDEΒΡ―”≥ΛœΏ”κACΒΡ―”≥ΛœΏΒΡΫΜΒψΘ°
Θ®1Θ©«σ÷ΛΘΚDE=EFΘΜ
Θ®2Θ©≈–ΕœBDΚΆCFΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τAB=3Θ§AE=![]() Θ§«σBDΒΡ≥ΛΘ°
Θ§«σBDΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy1=©¹x+2ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐy2=![]() ΒΡΆΦœσΫΜ”ΎΒψAΘ®©¹1Θ§3Θ©ΓΔBΘ®nΘ§©¹1Θ©Θ°
ΒΡΆΦœσΫΜ”ΎΒψAΘ®©¹1Θ§3Θ©ΓΔBΘ®nΘ§©¹1Θ©Θ°
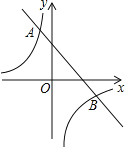
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±y1ΘΨy2 ±Θ§÷±Ϋ”–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com