练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一次函数y1=﹣x+2的图象与反比例函数y2=的图象交于点A（﹣1，3）、B（n，﹣1）．

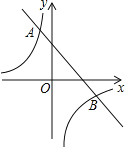
    （1）求反比例函数的解析式；

    （2）当y1＞y2时，直接写出x的取值范围．

    【答案】（1）y=﹣；（2）x＜﹣1或0＜x＜3，y1＞y2．

    【解析】

    试题分析：（1）把A点坐标代入可求出m的值，从而得到反比例函数解析式；

    （2）利用反比例函数解析式确定B点坐标，然后观察函数图象，写出一次函数图象在反比例函数图象上方所对应的自变量的取值范围即可．

    解：（1）把A（﹣1，3）代入可得m=﹣1×3=﹣3，

    所以反比例函数解析式为y=﹣；

    （2）把B（n，﹣1）代入y=﹣得﹣n=﹣3，解得n=3，则B（3，﹣1），

    所以当x＜﹣1或0＜x＜3，y1＞y2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若将边形边数增加1条，则它的内角和增加__________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（ ）

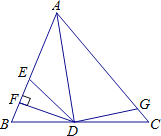
    A．11 B．5.5 C．7 D．3.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题是假命题的是( )

    A. 有一个角为60°的等腰三角形是等边三角形 B. 等角的补角相等

    C. 锐角三角形每个角都小于90° D. 内错角相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果关于x的一元二次方程x2+2ax+a+2=0有两个相等的实数根，那么实数a的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解全校七年级300名学生的视力情况，骆老师从中抽查了50名学生的视力情况．针对这个问题，下面说法正确的是（ ）

    A. 300名学生是总体 B. 每名学生是个体

    C. 50名学生是所抽取的一个样本 D. 这个样本容量是50

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在直角坐标平面内，抛物线y=x2+bx+c经过点A（2，0）、B（0，6）．

    （1）求抛物线的表达式；

    （2）抛物线向下平移几个单位后经过点（4，0）？请通过计算说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c交x轴于点A，B，交y轴于点C，点A的坐标是（﹣1，0），点C的坐标是（0，2）．

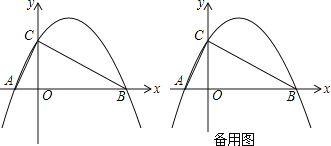
    （1）求该抛物线的解析式；

    （2）已知点P是抛物线的上的一个动点，点N在x轴上．

    ①若点P在x轴上方，且△APN是等腰直角三角形，求点N的坐标；

    ②若点P在x轴下方，且△ANP与△BOC相似，请直接写出点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，直线BC与x轴、y轴分别交于B、C两点，直线AD与x轴，y轴分别交于A、D两点，其中A（﹣3，0）、B（4，0），C（0，4）并且AD⊥BC于点E

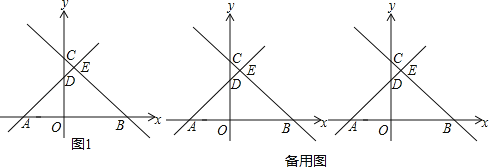
    （1）求点D的坐标；

    （2）点P从点A出发沿x轴正方向匀速运动，运动速度为每秒2个单位的长度，过点P作PM⊥x轴分别交直线AD、BC于点M、N，设点P的运动时间为t（秒），MN=m（m＞0），请用含t的式子表示m，并说明理由（并直接写出t的取值范围）；

    （3）在（2）的条件下，EK⊥x轴于点K，连接MK，作KQ⊥MK交直线BC于点Q，当S△KQB=时，求此时的P值及点M的坐标．

    查看答案和解析>>

    同步练习册答案