
【题目】如图1,在平面直角坐标系中,直线BC与x轴、y轴分别交于B、C两点,直线AD与x轴,y轴分别交于A、D两点,其中A(﹣3,0)、B(4,0),C(0,4)并且AD⊥BC于点E
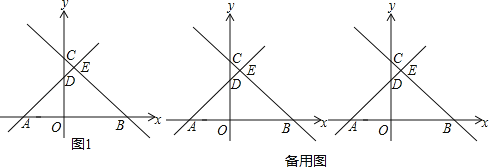
(1)求点D的坐标;
(2)点P从点A出发沿x轴正方向匀速运动,运动速度为每秒2个单位的长度,过点P作PM⊥x轴分别交直线AD、BC于点M、N,设点P的运动时间为t(秒),MN=m(m>0),请用含t的式子表示m,并说明理由(并直接写出t的取值范围);
(3)在(2)的条件下,EK⊥x轴于点K,连接MK,作KQ⊥MK交直线BC于点Q,当S△KQB=![]() 时,求此时的P值及点M的坐标.
时,求此时的P值及点M的坐标.
【答案】(1)(0,3)(2)答案见解析(3)p=﹣2, M(﹣2,1),
【解析】
试题分析:(1)设直线BC解析式为y=kx+b,把B与C坐标代入求出k与b的值,确定出直线BC解析式,由直线AE与直线BC垂直,以及A的坐标确定出直线AE解析式,即可求出D的坐标;
(2)联立直线AE与直线BC解析式,求出E坐标,确定出AK的长,分三种情况考虑:当0<t≤![]() 时;当
时;当![]() <t≤
<t≤![]() 时;当
时;当![]() <t≤
<t≤![]() 时,分别用t表示出m即可;
时,分别用t表示出m即可;
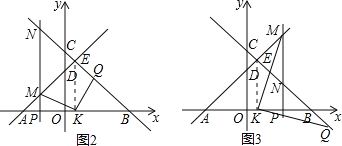
(3)如图2和图3所示,根据三角形BKQ的面积及KB的长,求出Q的纵坐标,进而求出横坐标,确定出Q坐标,分别设出P坐标,表示出M坐标,由MK与KQ垂直求出M坐标,进而求出P的坐标以及此时t的值即可.
解:(1)设直线BC解析式为y=kx+b,
把B(4,0),C(0,4)代入得:![]() ,
,
解得:![]() ,
,
故直线BC解析式为y=﹣x+4,
由直线AE⊥直线BC,得到直线AE解析式为y=x+a,
把A(﹣3,0)代入得:0=﹣3+a,即a=3,
故直线AE解析式为y=x+3,
令x=0,得到y=3,即D(0,3);
(2)过C作CK⊥x轴,如图2所示,
联立得:![]() ,
,
解得:![]() ,即E(
,即E(![]() ,
,![]() ),
),
∴AK=OA+OK=3![]() ,
,
分三种情况考虑:
当0<t≤![]() 时,由题意得:P(2t﹣3,0)
时,由题意得:P(2t﹣3,0)
把x=2t﹣3代入直线AE解析式得:PM=y=2t,把x=2t﹣3代入直线BC解析式得:PN=y=7﹣2t,
此时m=MN=PN﹣PM=7﹣2t﹣2t=7﹣4t;
当![]() <t≤
<t≤![]() 时,由题意得:OP=AP﹣AO=2t﹣3,
时,由题意得:OP=AP﹣AO=2t﹣3,
把x=2t﹣3代入直线AE解析式得:PM=y=2t,把x=2t﹣3代入直线BC解析式得:PN=7﹣2t,
此时m=MN=PN﹣PM=7﹣2t﹣2t=7﹣4t;
当![]() <t≤
<t≤![]() 时,由题意得:OP=AP﹣AO=2t﹣3,
时,由题意得:OP=AP﹣AO=2t﹣3,
把x=2t﹣3代入直线AE解析式得:PM=y=2t,把x=2t﹣3代入直线BC解析式得:PN=7﹣2t,
此时m=MN=PM﹣PN=2t﹣7+2t=4t﹣7;
(3)由(2)得:OK=![]() ,KB=OB﹣OK=4﹣
,KB=OB﹣OK=4﹣![]() =
=![]() ,
,
∵S△KQB=![]() ×KB×|yQ纵坐标|=
×KB×|yQ纵坐标|=![]() ×
×![]() ×|yQ纵坐标|=
×|yQ纵坐标|=![]() ,
,
∴|yQ纵坐标|=![]() ,
,
当yQ纵坐标=![]() 时,如图2所示,把y=
时,如图2所示,把y=![]() 代入直线BC解析式得:x=
代入直线BC解析式得:x=![]() ,即此时Q(
,即此时Q(![]() ,
,![]() );
);
设此时P(p,0),把x=p代入直线AE解析式得:PM=y=p+3,即M(p,p+3),
∵MK⊥KQ,K(![]() ,0),
,0),
∴kMK×kKQ=﹣1,即![]() ×
×![]() =﹣1,
=﹣1,
解得:p=﹣2,此时P(﹣2,0),M(﹣2,1),t=0.5;
当yQ纵坐标=﹣![]() 时,如图3所示,把y=﹣
时,如图3所示,把y=﹣![]() 代入直线BC解析式得:x=
代入直线BC解析式得:x=![]() ,即此时Q(
,即此时Q(![]() ,﹣
,﹣![]() );
);
设此时P(m,0),把x=m代入直线AE解析式得:PM=y=m+3,即M(m,m+3),
∵MK⊥KQ,K(![]() ,0),
,0),
∴kMK×kKQ=﹣1,即![]() ×
×![]() =﹣1,
=﹣1,
解得:m=3.
此时P(3,0),M(3,6),t=3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=![]() 的图象交于点A(﹣1,3)、B(n,﹣1).
的图象交于点A(﹣1,3)、B(n,﹣1).
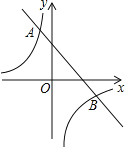
(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
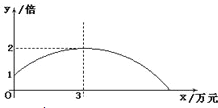
【题目】某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A. (2x+y)(2y+x) B. (x+1)(-x﹣1) C. (-x﹣y)(-x+y) D. (3x-y)(-3x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°;
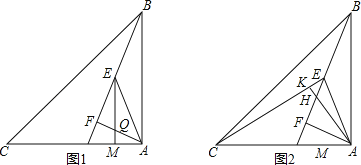
(1)如图1,EM∥AB,分别交AF、AD于点Q、M,求证:FD=FQ;
(2)如图2,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.
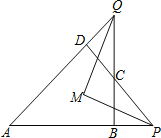
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣3,3).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
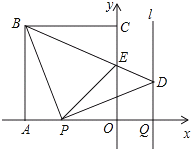
(1)求∠EBP的度数;
(2)求点D运动路径的长;
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com