
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°;
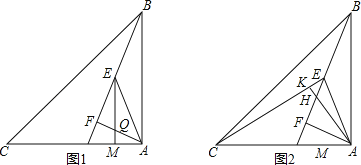
(1)如图1,EM∥AB,分别交AF、AD于点Q、M,求证:FD=FQ;
(2)如图2,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,求EC的长.
,求EC的长.
【答案】(1)证明见解析(2)6
【解析】
试题分析:(1)证得△ADF≌EQF,即可证得结论;
(2)延长AF交CE于P,证得△ABH≌△APC得出AH=CP,证得△AHF≌△EPF得出AH=EP,得出EC=2AH,解30°的直角三角形AFH求得AH,即可求得EC的长.
(1)证明:如图1,∵∠EAF=45°,AF⊥BD,
∴AF=EF,
∵EM∥AB,∠BAC=90°,
∴∠AME=90°,
∴∠AQM+∠FAD=90°,
∵∠ADF+∠FAD=90°,
∴∠AQM=∠ADF,
∴∠EQF=∠ADF,
在△ADF和EQF中,
 ,
,
∴△ADF≌EQF(AAS),
∴FD=FQ;
(2)解:如图2,延长AF交CE于P,
∵∠ABH+∠ADB=90°,∠PAC+∠ADB=90°,
∴∠ABH=∠PAC,
∵AK⊥CE,AF⊥BD,∠EHK=∠AHF,
∴∠HEK=∠FAH,
∵∠FAH+∠AHF=90°,∠HEK+∠EPF=90°,
∴∠AHF=∠EPF,
∴∠AHB=∠APC,
在△ABH与△APC中,
 ,
,
∴△ABH≌△APC(ASA),
∴AH=CP,
在△AHF与△EPF中,
 ,
,
∴△AHF≌△EPF(AAS),
∴AH=EP,∠CED=∠HAF,
∴EC=2AH,
∵∠DEC=30°,
∴∠HAF=30°,
∴AH=2FH=2×![]() =3,
=3,
∴EC=2AH=6.




科目:初中数学 来源: 题型:
【题目】已知在直角坐标平面内,抛物线y=x2+bx+c经过点A(2,0)、B(0,6).
(1)求抛物线的表达式;
(2)抛物线向下平移几个单位后经过点(4,0)?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线BC与x轴、y轴分别交于B、C两点,直线AD与x轴,y轴分别交于A、D两点,其中A(﹣3,0)、B(4,0),C(0,4)并且AD⊥BC于点E
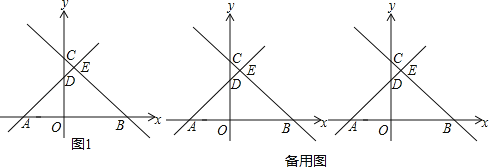
(1)求点D的坐标;
(2)点P从点A出发沿x轴正方向匀速运动,运动速度为每秒2个单位的长度,过点P作PM⊥x轴分别交直线AD、BC于点M、N,设点P的运动时间为t(秒),MN=m(m>0),请用含t的式子表示m,并说明理由(并直接写出t的取值范围);
(3)在(2)的条件下,EK⊥x轴于点K,连接MK,作KQ⊥MK交直线BC于点Q,当S△KQB=![]() 时,求此时的P值及点M的坐标.
时,求此时的P值及点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
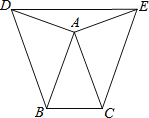
(1)求证:AB=AC;
(2)若∠DAE=2∠ABC=140°,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
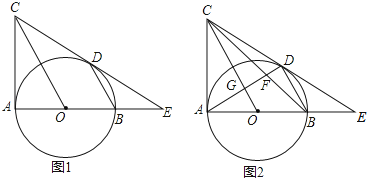
【题目】如图,∠BAC=90°,以AB为直径作⊙O,BD∥OC交⊙O于D点,CD与AB的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
(3)在(2)的条件下,如图2,AD交BC、OC分别于F、G,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“辽宁号”航母是中国海军航空母舰的首舰,标准排水量57000吨,满载排水量67500吨.数据67500用科学记数法表示为( )
A. 675×102 B. 67.5×103 C. 6.75×104 D. 6.75×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “打开电视机,它正在播广告”是必然事件
B. “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件
C. 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行
D. 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com