
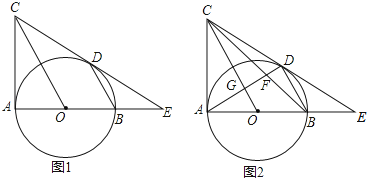
【题目】如图,∠BAC=90°,以AB为直径作⊙O,BD∥OC交⊙O于D点,CD与AB的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
(3)在(2)的条件下,如图2,AD交BC、OC分别于F、G,求![]() 的值.
的值.
【答案】(1)见解析;(2)CD=6;(3)![]() .
.
【解析】
试题分析:(1)连接OD,如图1,利用平行线的性质得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,于是可根据“SAS”判定△CDO≌△CAO,则∠CDO=∠CAO=90°,然后根据切线的判定定理可得到CD是⊙O的切线;
(2)设⊙O半径为r,则OD=OB=r,在Rt△ODE中利用勾股定理得到r2+42=(r+2)2,解得r=3,即OB=3,然后根据平行线分线段成比例定理,由DB∥OC得到DE:CD=BE:OB,于是可计算出CD=6;
(3)如图3,由△CDO≌△CAO得到AC=CD=6,在Rt△AOC中利用勾股定理计算出OC=3![]() ,再证明Rt△OAG∽△OCA,利用相似比计算出OG=
,再证明Rt△OAG∽△OCA,利用相似比计算出OG=![]() ,则CG=OC﹣OG=
,则CG=OC﹣OG=![]() ,易得BD=2OG=
,易得BD=2OG=![]() ,然后利用CG∥BD得到
,然后利用CG∥BD得到![]() =
=![]() =
=![]() .
.
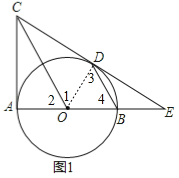
(1)证明:连接OD,如图1,
∵BD∥OC,
∴∠1=∠3,∠2=∠4,
又∵OD=OB,
∴∠3=∠4,
∴∠1=∠2,
在△CAO和△CDO中,
 ,
,
∴△CDO≌△CAO,
∴∠CDO=∠CAO=90°,
∴CD⊥OD,
∴CD是⊙O的切线;
(2)解:设⊙O半径为r,则OD=OB=r,
在Rt△ODE中,∵OD2+DE2=OE2,
∴r2+42=(r+2)2,解得r=3,
∴OB=3,
∵DB∥OC,
∴DE:CD=BE:OB,即4:CD=2:3,
∴CD=6;
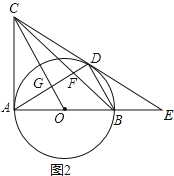
(3)解:如图3,
由(1)得△CDO≌△CAO,
∴AC=CD=6,
在Rt△AOC中,OC=![]() =
=![]() =3
=3![]() ,
,
∵∠AOG=∠COA,
∴Rt△OAG∽△OCA,
∴OA:OC=OG:OA,即3:3![]() =OG:3,
=OG:3,
∴OG=![]() ,
,
∴CG=OC﹣OG=3![]() ﹣
﹣![]() =
=![]() ,
,
∵OG∥BD,OA=OB,
∴OG为△ABD的中位线,
∴BD=2OG=![]() ,
,
∵CG∥BD,
∴![]() =
=![]() =
=![]() =
=![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
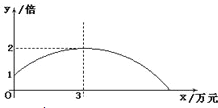
【题目】某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°;
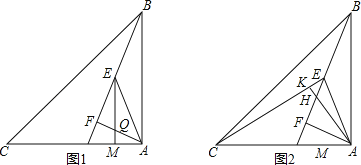
(1)如图1,EM∥AB,分别交AF、AD于点Q、M,求证:FD=FQ;
(2)如图2,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
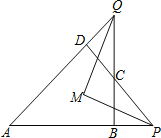
【题目】如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
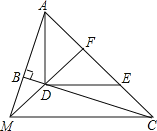
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com