
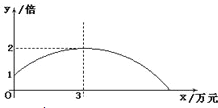
����Ŀ��ij��˾����һ�ֲ�Ʒ��ÿ����Ʒ�ijɱ��ۡ����ۼۼ��������������Ϊ�˻�ȡ���������˾����Ͷ��һ�����ʽ���������棬������֣�ÿ��Ͷ��Ĺ���Ϊx��Ԫ����Ʒ������������ԭ��������y������y��x�ĺ���ͼ��Ϊ��ͼ��ʾ��һ�������ߣ�
�ɱ��ۣ�Ԫ/���� | ���ۼۣ�Ԫ/���� | �����������/�£� |
2 | 3 | 9 |
��1����y��x�ĺ�����ϵʽΪ ���Ա���x��ȡֵ��ΧΪ ��
��2����֪������������ܶ��ȥ�ɱ��Ѻ��ѣ�Ҫʹÿ��������������ʹ�˾ӦͶ����ٹ��ѣ�
���𰸡���1��y=��![]() ��x��3��2+2��0��x��7.2����2��Ͷ��2.5����ѣ�
��x��3��2+2��0��x��7.2����2��Ͷ��2.5����ѣ�
��������
�����������1������������ͼ���ܹ�д��y��x�ĺ�����ϵʽ��Ȼ�����y=0ʱ��x��ֵ��
��2������������������ܶ��ȥ�ɱ��Ѻ��ѣ�д��������ϵʽ������������
�⣺��1����y��x�ĺ�����ϵʽΪy=a��x��b��2+c��
����ͼ���֪b=3��c=2��a=��![]() ��
��
��y=��![]() ��x��3��2+2��
��x��3��2+2��
��y=0�����x=7.2��
���Ա���x��ȡֵ��ΧΪ0��x��7.2��
��2����������������ܶ��ȥ�ɱ��Ѻ��ѣ����г�������ϵʽ
w=����x��3��2+18��x��
��w=��x2+5x+9��
��x=2.5ʱ���������
��Ͷ��2.5����ѣ�


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǽ��������( )
A. ��һ����Ϊ60���ĵ����������ǵȱ������� B. �ȽǵIJ������
C. ���������ÿ���Ƕ�С��90�� D. �ڴ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��![]() x2+bx+c��x���ڵ�A��B����y���ڵ�C����A�������ǣ���1��0������C�������ǣ�0��2����
x2+bx+c��x���ڵ�A��B����y���ڵ�C����A�������ǣ���1��0������C�������ǣ�0��2����
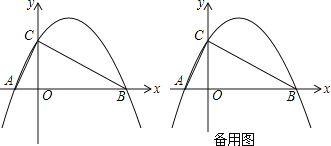
��1����������ߵĽ���ʽ��
��2����֪��P�������ߵ��ϵ�һ�����㣬��N��x���ϣ�
������P��x���Ϸ�������APN�ǵ���ֱ�������Σ����N�����ꣻ
������P��x���·�������ANP����BOC���ƣ���ֱ��д����N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y1=x+m��mΪ��������ͼ���뷴��������![]() ��kΪ������k��0����ͼ���ཻ��A��1��3����
��kΪ������k��0����ͼ���ཻ��A��1��3����
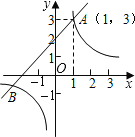
��1���������������Ľ���ʽ����ͼ�����һ����B�����ꣻ
��2���۲�ͼ��д��ʹ����ֵy1��y2���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȱ�������ABC�ı߳�Ϊ6����AC��BC���ϸ�ȡһ��E��F������AF��BE�ཻ�ڵ�P��

��1����AE=CF��
����֤��AF=BE��������APB�Ķ�����
����AE=2������APAF��ֵ��
��2����AF=BE������E�ӵ�A�˶�����Cʱ�������P������·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ��������ȷ���ǣ� ��.
A��x+x=x2 B����2x��2=4x C����x+1��2=x2+1 D��xx=x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��BC��x�ᡢy��ֱ���B��C���㣬ֱ��AD��x�ᣬy��ֱ���A��D���㣬����A����3��0����B��4��0����C��0��4������AD��BC�ڵ�E
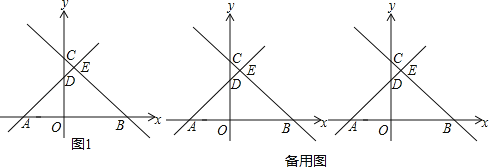
��1�����D�����ꣻ
��2����P�ӵ�A������x�������������˶����˶��ٶ�Ϊÿ��2����λ�ij��ȣ�����P��PM��x��ֱ�ֱ��AD��BC�ڵ�M��N�����P���˶�ʱ��Ϊt���룩��MN=m��m��0�������ú�t��ʽ�ӱ�ʾm����˵�����ɣ���ֱ��д��t��ȡֵ��Χ����
��3���ڣ�2���������£�EK��x���ڵ�K������MK����KQ��MK��ֱ��BC�ڵ�Q����S��KQB=![]() ʱ�����ʱ��Pֵ����M�����꣮
ʱ�����ʱ��Pֵ����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
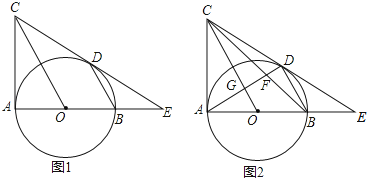
����Ŀ����ͼ����BAC=90������ABΪֱ������O��BD��OC����O��D�㣬CD��AB���ӳ��߽��ڵ�E��
��1����֤��CD����O�����ߣ�
��2����BE=2��DE=4����CD�ij���
��3���ڣ�2���������£���ͼ2��AD��BC��OC�ֱ���F��G����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��![]() x+4��x�ᡢy��ֱ���A��B���㣬��AOB�Ƶ�A˳ʱ����ת90���õ���AO��B�������B�Ķ�Ӧ��B������Ϊ�� ��
x+4��x�ᡢy��ֱ���A��B���㣬��AOB�Ƶ�A˳ʱ����ת90���õ���AO��B�������B�Ķ�Ӧ��B������Ϊ�� ��

A����3��4�� B����7��4�� C����7��3�� D����3��7��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com