
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
【答案】(1)①见解析;②12;(2)![]() 或3
或3![]() .
.
【解析】
试题分析:(1)①证明△ABE≌△CAF,借用外角即可以得到答案;②利用勾股定理求得AF的长度,再用平行线分线段成比例定理或者三角形相似定理求得![]() 的比值,即可以得到答案.
的比值,即可以得到答案.
(2)当点F靠近点C的时候点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,继而求得半径和对应的圆心角的度数,求得答案.点F靠近点B时,点P的路径就是过点B向AC做的垂线段的长度;
(1)①证明:∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,
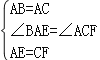 ,
,
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°﹣∠APE=120°.
②∵∠C=∠APE=60°,∠PAE=∠CAF,∴△APE∽△ACF,
∴![]() ,即
,即![]() ,所以APAF=12
,所以APAF=12
(2)若AF=BE,有AE=BF或AE=CF两种情况.
①当AE=CF时,点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,
又∵AB=6,
∴OA=![]() ,
,
点P的路径是![]() .
.
②当AE=BF时,点P的路径就是过点C向AB作的垂线段的长度;因为等边三角形ABC的边长为6,所以点P的路径为:![]() .
.
所以,点P经过的路径长为![]() 或3
或3![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
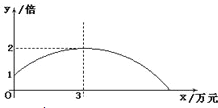
【题目】某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A. (2x+y)(2y+x) B. (x+1)(-x﹣1) C. (-x﹣y)(-x+y) D. (3x-y)(-3x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°;
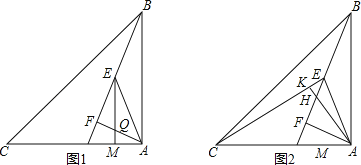
(1)如图1,EM∥AB,分别交AF、AD于点Q、M,求证:FD=FQ;
(2)如图2,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com