
【题目】如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.
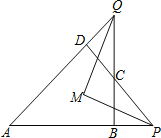
【答案】证明见解析
【解析】
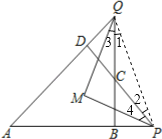
试题分析:连接PQ,由三角形内角和定理可得出∠QCP=180°﹣∠1﹣∠2,∠A=180°﹣∠AQP﹣∠APQ=180°﹣∠1﹣∠2﹣∠AQB﹣∠APD,再根据∠APD、∠AQB的平分线交于点M可知∠AQB=2∠3,∠APD=2∠4,再由三角形外角的性质可得出∠QMP=![]() (∠BCD+∠A),进而得出结论.
(∠BCD+∠A),进而得出结论.
证明:连接PQ,
∵∠QCP=180°﹣∠1﹣∠2,
∠A=180°﹣∠AQP﹣∠APQ=180°﹣∠1﹣∠2﹣∠AQB﹣∠APD,
又∵∠APD、∠AQB的平分线交于点M,
∴∠AQB=2∠3,∠APD=2∠4,
∴∠QCP+∠A=(180°﹣∠1﹣∠2)+(180°﹣∠1﹣∠2﹣2∠3﹣2∠4)
=360°﹣2∠1﹣2∠2﹣2∠3﹣2∠4,
∴![]() (∠QCP+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
(∠QCP+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
又∵∠BCD=∠QCP,
∴![]() (∠BCD+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
(∠BCD+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
又∵∠QMP=180°﹣∠MQP﹣∠MPQ=180°﹣∠1﹣∠3﹣∠2﹣∠4,
∴∠QMP=![]() (∠BCD+∠A)=
(∠BCD+∠A)=![]() ×180°=90°,即PM⊥QM.
×180°=90°,即PM⊥QM.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c交x轴于点A,B,交y轴于点C,点A的坐标是(﹣1,0),点C的坐标是(0,2).
x2+bx+c交x轴于点A,B,交y轴于点C,点A的坐标是(﹣1,0),点C的坐标是(0,2).
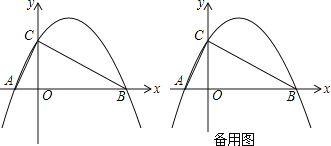
(1)求该抛物线的解析式;
(2)已知点P是抛物线的上的一个动点,点N在x轴上.
①若点P在x轴上方,且△APN是等腰直角三角形,求点N的坐标;
②若点P在x轴下方,且△ANP与△BOC相似,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线BC与x轴、y轴分别交于B、C两点,直线AD与x轴,y轴分别交于A、D两点,其中A(﹣3,0)、B(4,0),C(0,4)并且AD⊥BC于点E
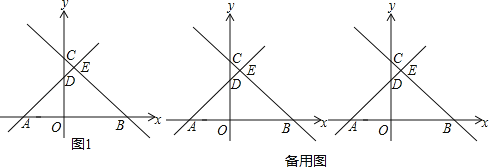
(1)求点D的坐标;
(2)点P从点A出发沿x轴正方向匀速运动,运动速度为每秒2个单位的长度,过点P作PM⊥x轴分别交直线AD、BC于点M、N,设点P的运动时间为t(秒),MN=m(m>0),请用含t的式子表示m,并说明理由(并直接写出t的取值范围);
(3)在(2)的条件下,EK⊥x轴于点K,连接MK,作KQ⊥MK交直线BC于点Q,当S△KQB=![]() 时,求此时的P值及点M的坐标.
时,求此时的P值及点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
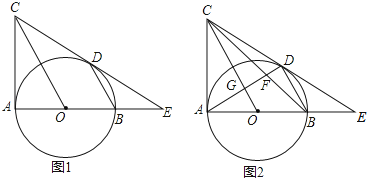
【题目】如图,∠BAC=90°,以AB为直径作⊙O,BD∥OC交⊙O于D点,CD与AB的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
(3)在(2)的条件下,如图2,AD交BC、OC分别于F、G,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“辽宁号”航母是中国海军航空母舰的首舰,标准排水量57000吨,满载排水量67500吨.数据67500用科学记数法表示为( )
A. 675×102 B. 67.5×103 C. 6.75×104 D. 6.75×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AEBE=CEED;③CA2=CECD;④CD=BD+AD.其中正确的个数是( )
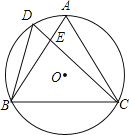
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “打开电视机,它正在播广告”是必然事件
B. “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件
C. 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行
D. 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于A、B两点,△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B的对应点B′坐标为( )
x+4与x轴、y轴分别交于A、B两点,△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B的对应点B′坐标为( )

A.(3,4) B.(7,4) C.(7,3) D.(3,7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com