
【题目】如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AEBE=CEED;③CA2=CECD;④CD=BD+AD.其中正确的个数是( )
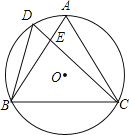
A.4 B.3 C.2 D.1
【答案】A
【解析】
试题分析:连接AD,根据等边三角形的性质得到∠BAC=∠ABC=60°,由圆周角定理得到∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,于是得到∠BDC=∠ADC=60°,故①正确;根据圆周角定理得到∠D=∠A,∠ABD=∠ACD,推出△BDE∽△ACE,根据相似三角形的性质即可得到AEBE=CEED;故②正确;由于∠ADC=∠EAC=60°,∠ACE=∠ACD,得到△ACD∽△ACE,根据相似三角形的性质得到CA2=CECD;故③正确;在CD上截取CF=BD,通过△ABD≌△ACF,得到AD=AF,推出△ADF是等边三角形,得到DF=AD,等量代换即可得到结论.
解:连接AD,∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,
∴∠BDC=∠ADC=60°,故①正确;
∵∠D=∠A,∠ABD=∠ACD,
∴△BDE∽△ACE,
∴![]() ,
,
∴AEBE=CEED;故②正确;
∵∠ADC=∠EAC=60°,∠ACE=∠ACD,
∴△ACD∽△ACE,
∴![]() ,
,
∴CA2=CECD;故③正确;
在CD上截取CF=BD,
在△ABD与△ACF中,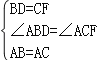 ,
,
∴△ABD≌△ACF,
∴AD=AF,
∵∠ADC=60°,
∴△ADF是等边三角形,
∴DF=AD,
∵CD=CF+DF,
∴CD=BD+AD.故④正确.
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )

A.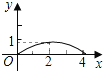 B.
B.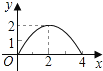
C.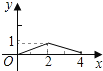 D.
D.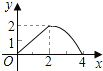
查看答案和解析>>
科目:初中数学 来源: 题型:
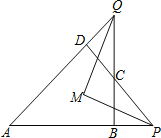
【题目】如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
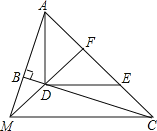
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com