
【题目】如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
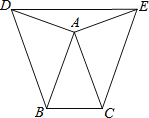
(1)求证:AB=AC;
(2)若∠DAE=2∠ABC=140°,求∠BAD的度数.
【答案】(1)证明见解析(2)90°
【解析】
试题分析:(1)由等腰三角形的性质可知∠ADE=∠AED,从而可得到∠ADB=∠AEC,依据AAS可证明△ADB≌△AEC;
(2)由题意可知:∠ABC=70°,由等腰三角形的性质可知∠ABC=∠ACB=70°,由三角形内角和定理可知∠BAC=40°,由△ADB≌△AEC可知∠DAB=∠EAC,故此∠BAD=![]() (360°﹣140°﹣40°)=90°.
(360°﹣140°﹣40°)=90°.
(1)证明:∵AD=AE,
∴∠ADE=∠AED.
∵∠BDE=∠CED,
∴∠BDE﹣∠ADE=∠CED﹣∠AED.
∴∠ADB=∠AEC.
在△ADB和△AEC中,
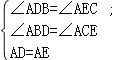
∴△ADB≌△AEC.
∴AB=AC.
(2)解:∵2∠ABC=140°,
∴∠ABC=70°.
∵AB=AC,
∴∠ABC=∠ACB=70°.
∴∠BAC=180°﹣∠ABC﹣∠ACB=40°.
∵△ADB≌△AEC,
∴∠DAB=∠EAC.
∵∠DAE=140°,
∴∠BAD=![]() (360°﹣140°﹣40°)=90°.
(360°﹣140°﹣40°)=90°.


科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A. (2x+y)(2y+x) B. (x+1)(-x﹣1) C. (-x﹣y)(-x+y) D. (3x-y)(-3x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=![]() ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
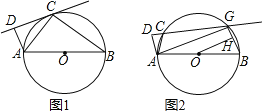
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,D为AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°;
(1)如图1,EM∥AB,分别交AF、AD于点Q、M,求证:FD=FQ;
(2)如图2,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
①abc>0;②a﹣b+c>0;③2a﹣3b=0;④c﹣4b>0.你认为其中正确信息是 (填序号).
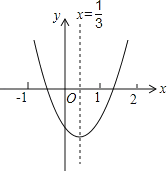
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一元二次方程x2﹣2x﹣a=0没有实数根,则一次函数y=(a+1)x+(a﹣1)的图象不过第( )
A.一象限 B.二象限 C.三象限 D.四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com