
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
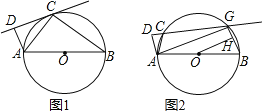
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
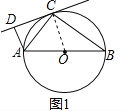
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=![]() ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.
【答案】
【解析】
试题分析:(1)首先连接OC,由CD切⊙O于C,根据切线的性质,可得OC⊥CD,又由AD⊥CD,可得OC∥AD,又由OA=OC,易证得∠DAC=∠CAO,根据圆周角定理求得∠ACB=90°,得出∠ADC=∠ACB,即可证得结论;
(2)由于四边形ABGC为⊙O的内接四边形,根据圆的内接四边形的性质得∠B+∠ACG=180°,易得∠ACD=∠B,又∠ADC=∠AGB=90°,利用等角的余角相等得到∠DAC=∠GAB,根据tan∠DAC=![]() =tan∠GAB=
=tan∠GAB=![]() 和勾股定理求得AG=8,GB=6,然后求得△ABG∽△OBH,根据相似三角形的性质求得
和勾股定理求得AG=8,GB=6,然后求得△ABG∽△OBH,根据相似三角形的性质求得![]() =
=![]() =
=![]() ,即可求得OH=4.
,即可求得OH=4.
(1)证明:连接OC,如图1,
∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB,
∴△ADC∽△ACB;
(2)解:如图2,∵AB是⊙O的直径,
∴∠AGB=90°,
∵四边形ABGC是⊙O的内接四边形,
∴∠ACD=∠B,
∵∠ADC=∠AGB=90°,
∴∠DAC=∠GAB,
∵tan∠DAC=![]() =tan∠GAB=
=tan∠GAB=![]() ,
,
设GB=3x,AG=4x,
∵AB=10,
∴(3x)2+(4x)2=102,
解得x=2,
∴AG=8,GB=6,
∵OH⊥GB,AG⊥GB,
∴OH∥AG,
∴△ABG∽△OBH,
∴![]() =
=![]() =
=![]() ,
,
∴OH=4.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】大树的价值很多,可以产生有毒气体,防止大气污染,增加土壤肥力,涵养水源,为鸟类及其他动物提供繁衍场所等价值,累计计算,一棵50年树龄的大树总计创造价值超过160万元,其中160万元用科学记数法表示为( )
A.1.6×105 B.1.6×106 C.1.6×107 D.1.6×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
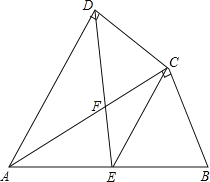
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
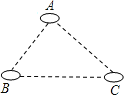
【题目】如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
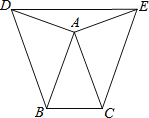
(1)求证:AB=AC;
(2)若∠DAE=2∠ABC=140°,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P1(-2,1)和P2(-2,-1),则P1和P2( )
A. 关于原点对称 B. 关于y轴对称 C. 关于x轴对称 D. 不存在对称关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com