
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
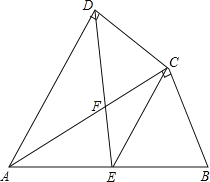
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值.
的值.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=ABAD;
(2)证明:∵E为AB的中点,
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=![]() AB,
AB,
∴CE=![]() ×6=3,
×6=3,
∵AD=4,
∴![]() ,
,
∴![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点A在m上,点B、C、D在n上,且AB=4cm,AC=5cm,AD=6cm,则m与n之间的距离( )
A. 等于5cm B. 等于6cm C. 等于4cm D. 小于或等于4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
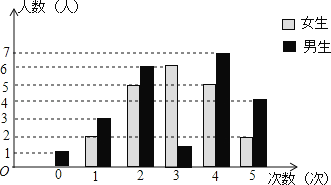
(1)该班级女生人数是 ;女生收看“两会”新闻次数的众数是 ;中位数是 .
(2)求女生收看次数的平均数.
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明计算出女生收看“两会”新闻次数的方差为![]() ,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
,男生收看“两会”新闻次数的方差为2,请比较该班级男、女生收看“两会”新闻次数的波动大小.
(4)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”,如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
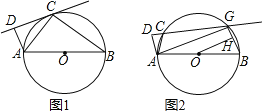
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=![]() ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com