
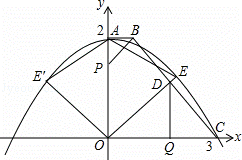
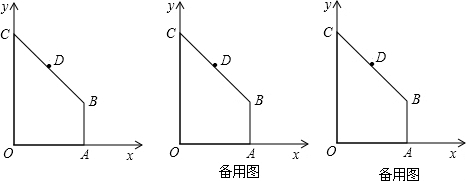
如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点O在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.
(1)求抛物线的解析式;
(2)点E′是E关于y轴的对称点,点Q运动到何处时,四边形OEAE′是菱形?
(3)点P、Q分别以每秒2个单位和3个单位的速度同时出发,运动的时间为t秒,当t为何值时,PB∥OD?
考点:
二次函数综合题.
分析:
(1)根据顶点式将A,C代入解析式求出a的值,进而得出二次函数解析式;
(2)利用菱形的性质得出AO与EE′互相垂直平分,利用E点纵坐标得出x的值,进而得出BC,EO直线解析式,再利用两直线交点坐标求法得出Q点坐标,即可得出答案;
(3)首先得出△APB∽△QDO,进而得出![]() =
=![]() ,求出m的值,进而得出答案.
,求出m的值,进而得出答案.
解答:
解:(1)∵A(0,2)为抛物线的顶点,
∴设y=ax2+2,
∵点C(3,0),在抛物线上,
∴9a+2=0,
解得:a=﹣![]() ,
,
∴抛物线为;y=﹣![]() x2+2;
x2+2;
(2)如果四边形OEAE′是菱形,则AO与EE′互相垂直平分,
∴EE′经过AO的中点,
∴点E纵坐标为1,代入抛物线解析式得:
1=﹣![]() x2+2,
x2+2,
解得:x=±![]()
![]() ,
,
∵点E在第一象限,
∴点E为(![]()
![]() ,1),
,1),
设直线BC的解析式为y=kx+b,把B(1,2),C(3,0),代入得:
![]() ,
,
解得:![]() ,
,
∴BC的解析式为:y=﹣x+3,
将E点代入y=ax,可得出EO的解析式为:y=![]() x,
x,
由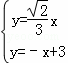 ,
,
得: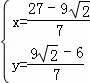 ,
,
∴Q点坐标为:(![]() ,0),
,0),
∴当Q点坐标为(![]() ,0)时,四边形OEAE′是菱形;
,0)时,四边形OEAE′是菱形;
(3)法一:设t为m秒时,PB∥DO,又QD∥y轴,则有∠APB=∠AOE=∠ODQ,
又∵∠BAP=∠DQO,则有△APB∽△QDO,
∴![]() =
=![]() ,
,
由题意得:AB=1,AP=2m,QO=3﹣3m,
又∵点D在直线y=﹣x+3上,∴DQ=3m,
因此:![]() =
=![]() ,解得:m=
,解得:m=![]() ,
,
经检验:m=![]() 是原分式方程的解,
是原分式方程的解,
∴当t=![]() 秒时,PB∥OD.
秒时,PB∥OD.
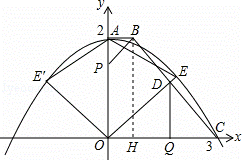
法二:作BH⊥OC于H,则BH=AO=2,OH=AB=1,HC=OC﹣OH=2,
∴BH=HC,∴∠BCH=∠CBH=45°,
易知DQ=CQ,
设t为m秒时PB∥OE,则△ABP∽△Q![]() OD,
OD,
∴![]() =
=![]()
![]() ,易知AP=2m,DQ=CQ=3m,QO=3﹣3m,
,易知AP=2m,DQ=CQ=3m,QO=3﹣3m,
∴![]() =
=![]() ,
,
解得m=![]() ,经检验m=
,经检验m=![]() 是方程的解,
是方程的解,
∴当t为![]() 秒时,PB∥OD.
秒时,PB∥OD.
点评:
此题主要考查了菱形的判定与性质以及顶点式求二次函数解析式以及相似三角形的判定与性质等知识,根据数形结合得出△APB∽△QDO是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,中位线EF分别交BD,AC于点G,H,∠ACB=30°,则下列结论中正确的有
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,中位线EF分别交BD,AC于点G,H,∠ACB=30°,则下列结论中正确的有查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
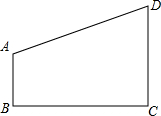 如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=4,BC=5
如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=4,BC=5| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•郴州)如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点Q在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.
(2013•郴州)如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点Q在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(51):34.4 二次函数的应用(解析版) 题型:解答题
 ,CD=9.
,CD=9.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com