
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(min) |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
分析 (1)根据信息二可列出关于小王每生产一件甲种产品和一件乙种产品分别需要的时间的方程组,解方程组即可.
(2)根据题意可以设出收入为y元,从而可以列出小王每月收入的关系式,再根据题目中的信息可知a≥60和每月工作25天列出相应的关系式,从而可以解答本题.
解答 解:(1)设小王每生产一件甲种产品和一件乙种产品分别需要x分钟、y分钟,则由题意得:
$\left\{\begin{array}{l}{10x+10y=350}\\{30x+20y=850}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=15}\\{y=20}\end{array}\right.$.
答:小王每生产一件甲种产品和一件乙种产品分别需要15分钟、20分钟.
(2)设小王每月的收入为y元,根据题意可得:
$\left\{\begin{array}{l}{y=1.5a+2.8b①}\\{15a+20b=25×[(12-8)+(17-13)]×60②}\\{a≥60③}\end{array}\right.$
由②得,3a+4b=2400.
∴b=$\frac{2400-3a}{4}$.
将b=$\frac{2400-3a}{4}$代入①,得
y=1680-0.6a.
∵a≥60,
∴当a=60时,y=1680-0.6a取得最大值,此时,y=1680-0.6×60=1644(元).
∴当收入最多时,a=60,b=$\frac{2400-3×60}{4}=555$.
答:小王每月生产甲产品a件,乙产品b件,当a、b分别60、555时,小王收入最多.
点评 本题考查了一次函数和二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 多项式 | p | q | a | b | 分解结果 |
| x2+9x+20 | 9 | 20 | 4 | 5 | (x+4)(x+5) |
| x2-9x+20 | -9 | 20 | -4 | -5 | (x-4)(x-5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
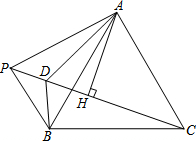 如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.
如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com