
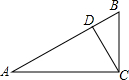
 如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.
如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长. 分析 过D作DE⊥AC于E,于是得到DE∥BC,根据平行线的性质得到∠CDE=∠BCD=30°,设CD=x,根据直角三角形的性质得到CE=$\frac{1}{2}$CD=$\frac{1}{2}$x,DE=$\frac{\sqrt{3}}{2}$x,求得AE=12-$\frac{1}{2}$x推出△ABC∽△ADE,根据相似三角形的性质得到$\frac{AC}{AE}=\frac{BC}{DE}$,列方程$\frac{12}{12-\frac{1}{2}x}=\frac{8}{\frac{\sqrt{3}}{2}x}$,即可得到结论.
解答 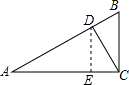 解:过D作DE⊥AC于E,
解:过D作DE⊥AC于E,
∵∠ACB=90°,
∴DE∥BC,
∴∠CDE=∠BCD=30°,
设CD=x,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$x,DE=$\frac{\sqrt{3}}{2}$x,
∴AE=12-$\frac{1}{2}$x,
∵DE∥BC,
∴△ABC∽△ADE,
∴$\frac{AC}{AE}=\frac{BC}{DE}$,
∴$\frac{12}{12-\frac{1}{2}x}=\frac{8}{\frac{\sqrt{3}}{2}x}$,
解得:x=$\frac{48(3\sqrt{3}-2)}{25}$.
∴CD=$\frac{48(3\sqrt{3}-2)}{25}$.
点评 本题考查了含30°角的直角三角形的性质,相似三角形的判定和性质,熟记含30°角的直角三角形的性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(min) |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
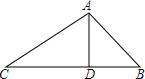 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com