练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
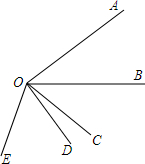
    20．如图，∠A0B=40°，∠B0E是任意一个小于平角的角，射线0C、0D分别平分∠A0E、∠B0E，求∠C0D的度数．

    分析 设∠BOE=x，先求得∠AOE=40°+x，由角平分线的定义可求得∠EOC=20°+$\frac{1}{2}x$，∠EOD=$\frac{1}{2}x$，最后依据∠COD=∠EOC-∠EOD求解即可．

    解答 解：设∠BOE=x．则∠AOE=∠AOB+∠BOE=40°+x．
    ∵射线0C、0D分别平分∠A0E、∠B0E，
    ∴∠EOC=20°+$\frac{1}{2}x$，∠EOD=$\frac{1}{2}x$．
    ∴∠DOC=∠EOC-∠EOD=20°+$\frac{1}{2}x$-$\frac{1}{2}x$=20°．

    点评 本题主要考查的是角平分线的定义，表示出∠EOC和∠EOD的度数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．已知x1、x2是方程x2-2（k+1）x+k2+2=0的另个实数根，且（x1+1）（x2+1）=8．求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如果-2x+7与-x-1互为相反数，则x的值为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

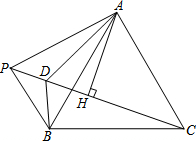    8．如图，P为等边△ABC外一点，AH垂直平分PC于点H，∠BAP的平分线交PC于点D．
    （1）求证：DP=DB；
    （2）求证：DA+DB=DC；
    （3）若等边△ABC边长为$\sqrt{14}$，连接BH，当△BDH为等边三角形时，请直接写出CP的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，△ABC中，∠ACB=90°，BC=8，AC=12，∠BCD=30°，求线段CD长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图所示，等边△ABC中，AD⊥BC于D．点P是AB边上的任意一点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC，垂足为E，过E作EF⊥AC，垂足为F，
    （1）如图1，证明：PE+2EF=2AD；
    （2）若AB=4，过F作FQ⊥AB，垂足为Q，PQ=1，求BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．六年级和七年级的学生参加一次乒乓球比赛，七年级的参赛人数是六年级的3倍，每两个参赛者都比赛一场且一定决出胜负．以所胜场次最多者为冠军，现知六年级学生所胜的场次数量与七年级学生所胜的场次数目相等．证明：冠军是六年级的学生．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．小丽想测量学校旗杆的高度，她在地面A点安置侧倾器，测得旗杆顶端C的仰角为α，侧倾器到旗杆底部的距离AD为10米，侧倾器的高度AB为1.5米，那么旗杆的高度CD为（　　）
    A．（10tanα+1.5）米B．（10cosα+1.5）米C．（$\frac{10}{tanα}$+1.5）米D．（$\frac{10}{sinα}$+1.5）米

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．试写出一个以-1，-3为两根的一元二次方程x2+4x+3=0．

    查看答案和解析>>

    同步练习册答案