练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    将两个斜边长相等的三角形纸片如图①放置，其中∠ACB=∠CED=90°，∠A=45°，∠D=30°．把△DCE绕点C顺时针旋转15°得到△D1CE1，如图②，连接D1B，则∠E1D1B的度数为（　　）

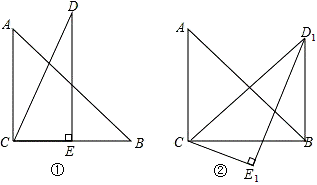
    　  A．10°         B． 20°            C． 7.5°           D． 15°


    D

    解：∵∠CED=90°，∠D=30°，∴∠DCE=60°，

    ∵△DCE绕点C顺时针旋转15°，∴∠BCE1=15°，

    ∴∠BCD1=60°﹣15°=45°，∴∠BCD1=∠A，

    在△ABC和△D1CB中，，∴△ABC≌△D1CB（SAS），

    ∴∠BD1C=∠ABC=45°，∴∠E1D1B=∠BD1C﹣∠CD1E1=45°﹣30°=15°．故选D．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，AB是⊙O的直径，点C在⊙O上，过点C作⊙O的切线CM．

    （1）求证：∠ACM=∠ABC；

    （2）延长BC到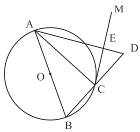D，使BC = CD，连接AD与CM交于点E，若⊙O的半径为3，ED = 2, 求∆ACE的外接圆的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线y=x+4与x轴、y轴分别交于A、B两点，把△A0B绕点A顺时针旋转90°后得到△AO′B′，则点B′的坐标是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    PM2.5是指大气中直径≤0.0000025米的颗粒物，将0.0000025用科学记数法表示为（　　）

    　  A．2.5×10﹣7     B． 2.5×10﹣6        C． 25×10﹣7         D． 0.25×10﹣5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个口袋中有4个完全相同的小球，它们的标号分别为1，2，3，4，从中随机摸出一个小球记下标号后放回，再从中随机摸出一个小球，则两次摸出的小球的标号之和大于4的概率是（　　）

    　  A．            B．                C．                D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简（1+）÷的结果为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


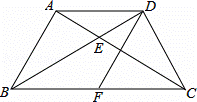
    如图，在四边形ABCD中，AB=AD，AC与BD交于点E，∠ADB=∠ACB．

    （1）求证：=；

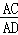    （2）若AB⊥AC，AE：EC=1：2，F是BC中点，求证：四边形ABFD是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


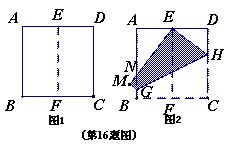
    如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF，如图2，展形再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为M，EM交AB于N，则tan∠ANE=      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知AB∥CD，∠C=65°，∠E=30°，则∠A的度数为（　　）

     

    　   A．30°                  B．                             32.5°                          C． 35°    D． 37.5°

    查看答案和解析>>

    同步练习册答案