Question

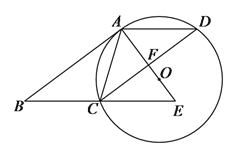
【题目】如图，在□ABCD中，AC=AD，⊙O是△ACD的外接圆，BC的延长线与AO的延长线交于E．

（1）求证：AB是⊙O的切线；

（2）若AB=8，AD=5，求OE的长.

Answer 1

【答案】（1）证明参见解析；（2）.

【解析】试题分析：（1）由已知得出弧AC=弧AD，由垂径定理得出OA⊥CD，由平行四边形的性质得出AB∥CD，AD∥BC，AD=BC，因此OA⊥AB，即可得出结论；（2）连接OD，由垂径定理得出CF=DF=4，由平行线得出△ADF∽△ECF，得出对应边成比例，证出AD=CE，AF=EF，得出BC=CE，BE=10，由勾股定理求出AE，得出AF=EF=3，设OE=x，则OF=3﹣x，⊙O的半径为6﹣x，由勾股定理得出方程，解方程即可．

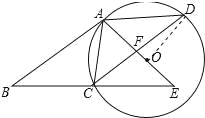
试题解析：（1）∵AC=AD，∴弧AC=弧AD，∴OA⊥CD，∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AD=BC，∴OA⊥AB，∴AB是⊙O的切线；（2）连接OD，如图所示：∵OA⊥CD，∴CF=DF=4，∵AD∥BC，∴△ADF∽△ECF，∴=1，∴AD=CE，AF=EF，∴BC=CE，∴BE=2BC=2AD=10，∴AE==6，∴AF=EF=3，设OE=x，则OF=3﹣x，⊙O的半径为6﹣x，由勾股定理得：OF2+DF2=OD2，即（6﹣x）2=（3﹣x）2+42，解得：x=，即OE=．