Question

【题目】如图，Rt△ABC中，∠C＝90o，O为AB上一点，以O为圆心，OB长为半径的圆，交BC边于点D，与AC边相切于点E．

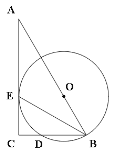
（1）求证：BE平分∠ABC；

（2）若CD︰BD＝1︰2，AC＝4，求CD的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

试题分析：（1）连接OE，根据OE=OB得出∠OEB=∠OBE，根据AC为切线得出∠OEA=90°，则∠C=∠OEA，从而得出OE∥BC，则∠OEB=∠EBC，从而得出∠OBE=∠EBC，得出角平分线；（2）过O作OF⊥BC于点F，连接OD，根据OD=OB，从而得出DF=BF，根据CD：BD=1：2，从而得出CD=DF=FB，从而得出四边形OECF为矩形，则CF=EO，从而得出△ODB为等边三角形，然后根据AC的长度得出BC的长度，从而得出CD的长度．

试题解析：（1）连接OE ∵OE＝OB ∴∠OEB＝∠OBE ∵AC与⊙O相切 ∴OE⊥AC，即∠OEA＝90°

∴∠C＝∠OEA＝90° ∴OE∥BC ∴∠OEB＝∠EBC ∴∠OBE＝∠EBC 即BE平分∠ABC

（2）过O作OF⊥BC于点F，连接OD ∵OD＝OB ∴DF＝BF ∵CD︰BD＝1︰2 ∴CD＝DF＝FB

∵四边形OECF为矩形 ∴CF＝EO ∴OE＝BD＝OD＝OB ∴△ODB为等边三角形 ∴∠ABC＝60°

∵AC＝4 ∴BC＝ ∴CD＝×BC＝