
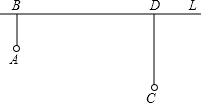
 如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km.
如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km.分析 (1)可作点A关于直线L的对称点A′,连接A′C与L相交于点P,点P即为所求;
(2)过点A′作AE垂直CD的延长线与点E,利用勾股定理求出线段A′C的长即可.
解答 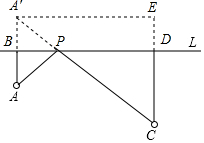 解:(1)如图,点P即为所求点;
解:(1)如图,点P即为所求点;
(2)由作图可得最短路程为A′C的距离,过A′作A′E⊥CD,交CD的延长线于E,
∵AB=2km,CD=4km且,BD=8km,
∴DE=A′B=AB=2km,A′E=BD=8km,CE=2+4=6km,
∴A′C=$\sqrt{A′{E}^{2}+C{E}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10km.
点评 本题考查的是作图-应用与设计作图,轴对称-最短路线问题以及轴对称图形在实际生活中的应用,但轴对称图形的画法、两点之间线段最短是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
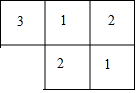 图是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在该位置小正方体的个数,请画出这个几何体从正面和从左面看到的形状图.
图是由几个大小相同的小正方体所搭成的几何体从上面看到的形状图,小正方形中的数字表示在该位置小正方体的个数,请画出这个几何体从正面和从左面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为5.
如图,已知正方形ABCD的边长为6,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=2,则FM的长为5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com