
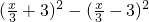
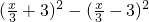 =(
=( +3+
+3+ -3)(
-3)( +3-
+3- +3)=12×
+3)=12× =4x;
=4x;

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.
四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,深加工产品占
,深加工产品占 .由于在国际市场上,初级产品的价格较低,不利于出口创汇,所以加入WTO后,必须尽快改变这种出口结构.假设我国每年的农产品的出口总量不变,两年后将深加工产品比重提高到
.由于在国际市场上,初级产品的价格较低,不利于出口创汇,所以加入WTO后,必须尽快改变这种出口结构.假设我国每年的农产品的出口总量不变,两年后将深加工产品比重提高到 ,那么平均每年比上一年提高的百分数是多少?(结果精确到0.1%,下列数据可供使用:
,那么平均每年比上一年提高的百分数是多少?(结果精确到0.1%,下列数据可供使用: ≈2.236,
≈2.236, ≈2.449).
≈2.449).查看答案和解析>>
科目:初中数学 来源: 题型:单选题
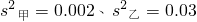 ,则下列判断正确的是
,则下列判断正确的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com