
 ,tanC=
,tanC=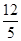 .点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
.点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
 与
与 的函数关系式,并写出函数定域义;
的函数关系式,并写出函数定域义; CF,联结DF.
CF,联结DF.
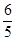 x+15 定义域0﹤x≦
x+15 定义域0﹤x≦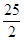 .(2)①⊙D的半径为
.(2)①⊙D的半径为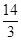 或
或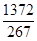 ,②⊙D的半径为
,②⊙D的半径为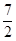 。
。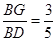 ,∵BD=x,∴BG=
,∵BD=x,∴BG=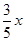 (1分)
(1分)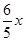 ,∵AB=15,∴y=15-
,∵AB=15,∴y=15-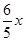 (1分)
(1分)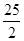 (1分)
(1分)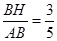

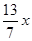 ,DC=14-x
,DC=14-x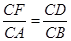 ,即
,即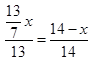 ,x=
,x=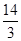 ,∴BD=
,∴BD=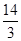 (1分)
(1分)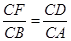 ,即
,即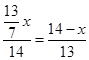 ,x=
,x=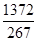 ,∴BD=
,∴BD=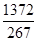 (1分)
(1分)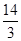 或
或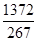
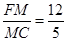 (1分)
(1分)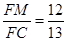 ,∵CF=
,∵CF=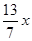 ,∴FM=
,∴FM=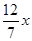 ,MC=
,MC=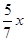 (1分)
(1分)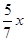 =14-
=14-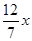 (1分)
(1分)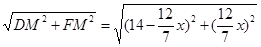 (1分)
(1分)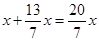 (1分)
(1分)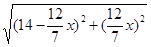 =
=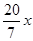 ,解得x1=
,解得x1=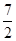 ,x2=
,x2=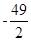 (舍去)
(舍去)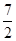 (1分)
(1分)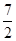 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com