
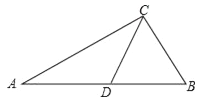
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=8ЃЌcosA=![]() ЃЌDЪЧABБпЕФжаЕуЃЌEЪЧACБпЩЯвЛЕуЃЌСЊНсDEЃЌЙ§ЕуDзїDFЁЭDEНЛBCБпгкЕуFЃЌСЊНсEFЃЎ
ЃЌDЪЧABБпЕФжаЕуЃЌEЪЧACБпЩЯвЛЕуЃЌСЊНсDEЃЌЙ§ЕуDзїDFЁЭDEНЛBCБпгкЕуFЃЌСЊНсEFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБDEЁЭACЪБЃЌЧѓEFЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкACБпЩЯвЦЖЏЪБЃЌЁЯDFEЕФе§ЧажЕЪЧЗёЛсЗЂЩњБфЛЏЃЌШчЙћБфЛЏЧыЫЕГіБфЛЏЧщПіЃЛШчЙћБЃГжВЛБфЃЌЧыЧѓГіЁЯDFEЕФе§ЧажЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌСЊНсCDНЛEFгкЕуQЃЌЕБЁїCQFЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіBFЕФГЄЃЎ
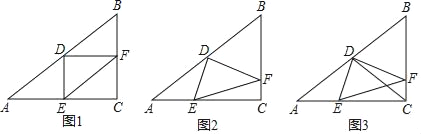
ЁОД№АИЁПЃЈ1ЃЉEF=5ЃЛЃЈ2ЃЉВЛБфЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉBFЕФГЄЮЊ3Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩcosA=![]() ЃЌИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхПЩЧѓПЩЧѓAC=8ЃЌAE=4ЃЌдкRtЁїEDFжаЃЌгЩЙДЙЩЖЈРэЧѓГіDE=3ЃЌдкRtЁїAEDжаЃЌгЩЙДЙЩЖЈРэЧѓГіEFЕФГЄЃЛ
ЃЌИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхПЩЧѓПЩЧѓAC=8ЃЌAE=4ЃЌдкRtЁїEDFжаЃЌгЩЙДЙЩЖЈРэЧѓГіDE=3ЃЌдкRtЁїAEDжаЃЌгЩЙДЙЩЖЈРэЧѓГіEFЕФГЄЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDHЁЭACЃЌDGЁЭBCЃЌДЙзуЗжБ№ЮЊЕуHЁЂGЃЌгЩЃЈ1ЃЉПЩЕУDH=3ЃЌDG=4ЃЌдйжЄЁїEDHЁзЁїFDGЃЌЕУЕН![]() ,ШЛКѓИљОне§ЧаЖЈвхЧѓНтЃЛ
,ШЛКѓИљОне§ЧаЖЈвхЧѓНтЃЛ
ЃЈ3ЃЉЗжQF=QCЃЌFQ=FCЃЌCF=CQШ§жжЧщПіЧѓНт.
НтЃКЃЈ1ЃЉЁпЁЯACB=90ЁуЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
ЁпAC=8ЃЌ
ЁрAB=10ЃЌ
ЁпDЪЧABБпЕФжаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпDEЁЭACЃЌ
ЁрЁЯDEA=ЁЯDEC=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=4ЃЌ
ЁрCE=8Љ4=4ЃЌ
ЁпдкRtЁїAEDжаЃЌAE2+DE2=AD2ЃЌ
ЁрDE=3ЃЌ
ЁпDFЁЭDEЃЌ
ЁрЁЯFDE=90ЁуЃЌ
гжЁпЁЯACB=90ЁуЃЌ
ЁрЫФБпаЮDECFЪЧОиаЮЃЌ
ЁрDF=EC=4ЃЌ
ЁпдкRtЁїEDFжаЃЌDF2+DE2=EF2ЃЌ
ЁрEF=5
ЃЈ2ЃЉВЛБф
ШчЭМ2ЃЌ

Й§ЕуDзїDHЁЭACЃЌDGЁЭBCЃЌДЙзуЗжБ№ЮЊЕуHЁЂGЃЌ
гЩЃЈ1ЃЉПЩЕУDH=3ЃЌDG=4ЃЌ
ЁпDHЁЭACЃЌDGЁЭBCЃЌ
ЁрЁЯDHC=ЁЯDGC=90Ёу
гжЁпЁЯACB=90ЁуЃЌ
ЁрЫФБпаЮDHCGЪЧОиаЮЃЌ
ЁрЁЯHDG=90ЁуЃЌ
ЁпЁЯFDE=90ЁуЃЌ
ЁрЁЯHDGЉЁЯHDF=ЁЯEDFЉЁЯHDFЃЌ
МДЁЯEDH=ЁЯFDGЃЌ
гжЁпЁЯDHE=ЁЯDGF=90Ёу
ЁрЁїEDHЁзЁїFDGЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯFDE=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈ3ЃЉЂйЕБQF=QCЪБЃЌ
ЁрЁЯQFC=ЁЯQCFЃЌ
ЁпЁЯEDF+ЁЯECF=180ЁуЃЌ
ЁрЕуDЃЌEЃЌCЃЌFЫФЕуЙВдВЃЌ
ЁрЁЯECQ=ЁЯDFEЃЌЁЯDFE+ЁЯQFC=ЁЯECQ+ЁЯQCF=ЁЯACB=90ЁуЃЌ
МДЁЯDFC=90ЁуЃЌ
гжЁпЁЯACB=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂкЕБFQ=FCЪБЃЌ
ЁрЁЯBCD=ЁЯCQFЃЌ
ЁпЕуDЪЧABЕФжаЕуЃЌ
ЁрBD=CD=![]() AB=5ЃЌ
AB=5ЃЌ
ЁрЁЯBDC=ЁЯBCDЃЌ
ЁрЁЯBCD=ЁЯFCQЃЌЁЯBDC=ЁЯCFQЃЌ
ЁрЁїFQCЁзЁїDCBЃЌ
гЩЂйжЊЃЌЕуDЃЌEЃЌCЃЌFЫФЕуЙВдВЃЌ
ЁрЁЯDEF=ЁЯDCFЃЌ
ЁпЁЯDQE=ЁЯFQCЃЌ
ЁрЁїFQCЁзЁїDEQЃЌ
МДЃКЁїFQCЁзЁїDEQЁзЁїDCB
ЁпдкRtЁїEDFжаЃЌ![]() ЃЌ
ЃЌ
ЁрЩшDE=3kЃЌдђDF=4kЃЌEF=5kЃЌ
ЁпЁЯDEF=ЁЯDCF=ЁЯCQF=ЁЯDQEЃЌ
ЁрDE=DQ=3kЃЌ
ЁрCQ=5Љ3kЃЌ
ЁпЁїDEQЁзЁїDCBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁїFQCЁзЁїDCBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр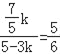 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂлЕБCF=CQЪБЃЌШчЭМ3ЃЌ

ЁрЁЯBCD=ЁЯCQFЃЌ
гЩЂкжЊЃЌCD=BDЃЌ
ЁрЁЯBDC=ЁЯBCDЃЌ
ЁпЁїEDQЁзЁїBDKЃЌ
дкBCБпЩЯНиШЁBK=BD=5ЃЌЙ§ЕуDзїDHЁЭBCгкHЃЌ
ЁрDH=![]() AC=4ЃЌBH=
AC=4ЃЌBH=![]() BC=3ЃЌгЩЙДЙЩЖЈРэЕУ
BC=3ЃЌгЩЙДЙЩЖЈРэЕУ![]() ЃЌ
ЃЌ
ЭЌЂкЕФЗНЗЈЕУЃЌЁїCFQЁзЁїEDQЃЌ
ЁрЩшDE=3mЃЌдђEQ=3mЃЌEF=5mЃЌ
ЁрFQ=2mЃЌ
ЁпЁїEDQЁзЁїBDKЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрDQ=![]() mЃЌ
mЃЌ
ЁрCQ=FC=5Љ![]() mЃЌ
mЃЌ
ЁпЁїCQFЁзЁїBDKЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр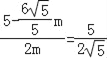 ЃЌ
ЃЌ
НтЕУm=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
МДЃКЁїCQFЪЧЕШбќШ§НЧаЮЪБЃЌBFЕФГЄЮЊ3Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 гХЩњРждАЯЕСаД№АИ
гХЩњРждАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌЕуFДгСтаЮABCDЕФЖЅЕуAГіЗЂЃЌбиAЁњDЁњBвд1cm/sЕФЫйЖШдШЫйдЫЖЏЕНЕуB.ЭМЂкЪЧЕуFдЫЖЏЪБЃЌЁїFBCЕФУцЛ§yЃЈcm![]() ЃЉЫцЪБМфxЃЈsЃЉБфЛЏЕФЙиЯЕЭМЯѓЃЌдђaЕФжЕЪЧ__
ЃЉЫцЪБМфxЃЈsЃЉБфЛЏЕФЙиЯЕЭМЯѓЃЌдђaЕФжЕЪЧ__
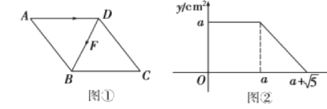
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌCDЪЧБпABЩЯЕФжаЯпЃЌЁЯBЪЧШёНЧЃЌЧвsinB=![]() ЃЌtanA=
ЃЌtanA=![]() ЃЌBC=2
ЃЌBC=2![]() ЃЌЧѓБпABЕФГЄКЭcosЁЯCDBЕФжЕЃЎ
ЃЌЧѓБпABЕФГЄКЭcosЁЯCDBЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћАбвЛИіздШЛЪ§ИїЪ§ЮЛЩЯЕФЪ§зжДгзюИпЮЛЕНИіЮЛвРДЮХХГіЕФвЛДЎЪ§зжЃЌгыДгИіЮЛЕНзюИпЮЛвРДЮХХГіЕФвЛДЎЪ§зжЭъШЋЯрЮЪЃЌФЧУДЮвУЧАбетбљЕФздШЛЪ§ГЦЮЊЁАКЭаГЪ§ЁБЃЌР§ШчздШЛЪ§12321ЃЌДгзюИпЮЛЕНИіЮЛвРДЮХХГіЕФвЛДЎЪ§зжЪЧЃК1ЁЂ2ЁЂ3ЁЂ2ЁЂ1ЃЌДгИіЮЛЕНзюИпЮЛвРДЮГіЕФвЛДЎЪ§зжШдЪЧЃК1ЁЂ2ЁЂ3ЁЂ2ЁЂ1ЃЌвђДЫ12321ЪЧвЛИіЁАКЭаГЪ§ЁБ.дйШч22ЁЂ545ЁЂ3883ЁЂ345543ЁЂЁЃЌЖМЪЧЁАКЭаГЪ§ЁБ.
(1)ЧыФужБНгаДГі3ИіЫФЮЛЁАКЭаГЪ§ЁБЃК_________________________________ЃЛ
(2)ЩшЫФЮЛЁАКЭаГЪ§ЁБИіЮЛЩЯЕФЪ§зжЮЊaЃЌЪЎЮЛЩЯЕФЪ§зжЮЊbЃЌЧыФуВТЯыШЮвтвЛИіЫФЮЛЁАКЭаГЪ§ЁБФмЗёБЛ11ећГ§?ВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇЪЧвЛУХГфТњРжШЄЕФбЇПЦЃЌФГаЃЦпФъМЖаЁПЭЌбЇЕФЪ§бЇбЇЯАаЁзщгіЕНвЛИіИЛгаЬєеНадЕФЬНхГЮЪЬтЃЌЧыФуАяжњЫћУЧЭъГЩећИіЬНОПЙ§ГЬЃЛ
ЃЈЮЪЬтБГОАЃЉ
ЖдгквЛИіе§ећЪ§nЃЌЮвУЧНјааШчЯТВйзїЃК
ЃЈ1ЃЉНЋnВ№ЗжЮЊСНИіе§ећЪ§m1ЃЌm2ЕФКЭЃЌВЂМЦЫуГЫЛ§m1ЁСm2ЃЛ
ЃЈ2ЃЉЖдгке§ећЪ§m1ЃЌm2ЃЌЗжБ№жиИДДЫВйзїЃЌЕУЕНСэЭтСНИіГЫЛ§ЃЛ
ЃЈ3ЃЉжиИДЩЯЪіЙ§ГЬЃЌжБжСВЛФмдйВ№ЗжЮЊжЙЃЌЃЈМДелЗжЕНе§ећЪ§1ЃЉЃЛ
ЃЈ4ЃЉНЋЫљгаЕФГЫЛ§ЧѓКЭЃЌВЂНЋЫљЕУЕФЪ§жЕГЦЮЊИУе§ећЪ§ЕФЁАЩёУижЕЁБЃЌ
ЧыЬНОПВЛЭЌЕФВ№ЗжЗНЪНЪЧЗёгАЯье§ећЪ§nЕФЁАЩёУижЕЁБЃЌВЂЫЕУїРэгЩЃЎ
ЃЈГЂЪдЬНОПЃЉЃК
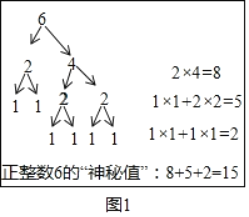

ЃЈ1ЃЉе§ећЪ§1КЭ2ЕФЁАЩёУижЕЁБЗжБ№ЪЧ
ЃЈ2ЃЉЮЊСЫбаОПвЛАуЕФЙцТЩЃЌаЁПЫљдкбЇЯАаЁзщЭЈЙ§ЬжТлЃЌОіЖЈдйбЁдёСНИіОпЬхЕФе§ећЪ§6КЭ7ЃЌжиИДЩЯЪіЙ§ГЬ
ЬНОПНсТлЃК
ШчЭМЫљЪОЃЌЪЧаЁПбЁдёЕФвЛжжВ№ЗжЗНЪНЃЌЭЈЙ§ИУВ№ЗжЗНЗЈЕУЕНе§ећЪ§6ЕФЁАЩёУижЕЁБЮЊ15ЃЎ
ЧыФЃЗТаЁПЕФМЦЫуЗНЪНЃЌдкШчЭМжаЃЌбЁдёСэЭтвЛжжВ№ЗжЗНЪНЃЌИјГіМЦЫуе§ећЪ§6ЕФЁАЩёУижЕЁБЕФЙ§ГЬЃЛЖдгке§ећЪ§7ЃЌЧыбЁдёвЛжжВ№ЗжЗНЪНЃЌдкШчЭМжачЊГіМЦЫуе§ећЪ§7ЕФЁАЩёУижЕЁБЕФЙ§ГЬЃЎ
ЃЈНсТлВТЯыЃЉ
НсКЯЩЯУцЕФЪЕМљЛюЖЏЃЌНјааИќЖрЕФГЂЪдКѓЃЌаЁПЫљдкбЇЯАаЁзщВТВтЃЌе§ећЪ§nЕФЁАЩёУижЕЁБгыЦфелЗжЗНЗЈЮоЙиЃЎЧыАяжњаЁПЃЌРћгУГЂЪдГЩЙћЃЌВТЯые§ећЪ§nЕФЁАЩёУижЕЁБЕФБэДяЪНЮЊ ЃЌЃЈгУКЌзжФИnЕФДњЪ§ЪНБэЪОЃЌжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтВЂНтД№ЃК
(1)ЮвУЧАбЖрЯюЪН![]() МА
МА![]() НазіЭъШЋЦНЗНЪНЃЌдкдЫгУЭъШЋЦНЗНЙЋЪННјаавђЪНЗжНтЪБЃЌЙиМќЪЧХаЖЯетИіЖрЯюЪНЪЧВЛЪЧвЛИіЭъШЋЦНЗНЪН.ЭЌбљЕиЃЌАбвЛИіЖрЯюЪННјааВПЗжвђЪНЗжНтПЩвдРДНтОіЧѓДњЪ§ЪНжЕЕФзюДѓ(ЛђзюаЁ)жЕЮЪЬт.
НазіЭъШЋЦНЗНЪНЃЌдкдЫгУЭъШЋЦНЗНЙЋЪННјаавђЪНЗжНтЪБЃЌЙиМќЪЧХаЖЯетИіЖрЯюЪНЪЧВЛЪЧвЛИіЭъШЋЦНЗНЪН.ЭЌбљЕиЃЌАбвЛИіЖрЯюЪННјааВПЗжвђЪНЗжНтПЩвдРДНтОіЧѓДњЪ§ЪНжЕЕФзюДѓ(ЛђзюаЁ)жЕЮЪЬт.
Р§ШчЃКЂй![]()
Ёп![]() ЪЧЗЧИКЪ§ЃЌМД
ЪЧЗЧИКЪ§ЃЌМД![]() Ён0
Ён0
Ёр![]() +2Ён2
+2Ён2
дђетИіДњЪ§ЪН![]() ЕФзюаЁжЕЪЧ_______ЃЌетЪБЯргІЕФ
ЕФзюаЁжЕЪЧ_______ЃЌетЪБЯргІЕФ![]() ЕФжЕЪЧ_______.
ЕФжЕЪЧ_______.
Ђк![]()
=![]()
=![]()
=![]()
=![]()
Ёп![]() ЪЧЗЧИКЪ§ЃЌМД
ЪЧЗЧИКЪ§ЃЌМД![]() Ён0
Ён0
Ёр![]() -7Ён-7
-7Ён-7
дђетИіДњЪ§ЪН![]() ЕФзюаЁжЕЪЧ____ЃЌетЪБЯргІЕФ
ЕФзюаЁжЕЪЧ____ЃЌетЪБЯргІЕФ![]() ЕФжЕЪЧ______.
ЕФжЕЪЧ______.
(2)ЗТееЩЯЪіЗНЗЈЧѓДњЪ§ЪН ![]() ЕФзюДѓ(ЛђзюаЁ)жЕЃЌВЂаДГіЯргІЕФ
ЕФзюДѓ(ЛђзюаЁ)жЕЃЌВЂаДГіЯргІЕФ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cНЛxжсгкA(-4ЃЌ0),BЃЈ1ЃЌ0),НЛyжсгкCЕуЃЌЧвOC=2OB.

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкжБЯпBCЩЯевЕуDЃЌЪЙЁїABDЮЊвдABЮЊбќЕФЕШбќШ§НЧаЮЃЌЧѓDЕуЕФзјБъЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдквьгкBЕФЕуPЃЌЙ§PЕузїPQЁЭACгкQЃЌЪЙЁїAPQгыЁїABCЯрЫЦЃПШєДцдкЃЌЧыЧѓГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈ2m+1ЃЉx2+4mx+2mЉ3=0
ЃЈЂёЃЉЕБm=![]() ЪБЃЌЧѓЗНГЬЕФЪЕЪ§ИљЃЛ
ЪБЃЌЧѓЗНГЬЕФЪЕЪ§ИљЃЛ
ЃЈЂђЃЉШєЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжабыЕчЪгЬЈЕФЁАРЪЖСепЁБНкФПМЄЗЂСЫЭЌбЇУЧЕФЖСЪщШШЧщЃЌЮЊСЫв§ЕМбЇЩњЁАЖрЖСЪщЃЌЖСКУЪщЁБЃЌФГаЃЖдАЫФъМЖВПЗжбЇЩњЕФПЮЭтдФЖССПНјааСЫЫцЛњЕїВщЃЌећРэЕїВщНсЙћЗЂЯжЃЌбЇЩњПЮЭтдФЖСЕФБОЪщзюЩйЕФга5БОЃЌзюЖрЕФга8БОЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫВЛЭъећЕФЭМБэЃЌШчЭМЫљЪОЃК
БОЪ§ЃЈБОЃЉ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
КЯМЦ | c | 1 |
ЃЈ1ЃЉЭГМЦБэжаЕФa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЌc=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыНЋЦЕЪ§ЗжВМБэжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЧѓЫљгаБЛЕїВщбЇЩњПЮЭтдФЖСЕФЦНОљБОЪ§ЃЛ
ЃЈ4ЃЉШєИУаЃАЫФъМЖЙВга1200УћбЇЩњЃЌЧыФуЗжЮіИУаЃАЫФъМЖбЇЩњПЮЭтдФЖС7БОМАвдЩЯЕФШЫЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com