
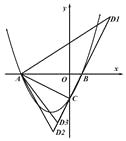
【题目】如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为![]() ;
;
(2)满足条件的D点有D1 ![]() ,D2
,D2![]() ,D3(1,4);
,D3(1,4);
(3)满足条件的点P有P![]() 和P′
和P′![]()
【解析】解:(1)依题意得, 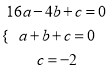 ,解得,
,解得, 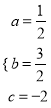 ,
,
 ∴抛物线的解析式为
∴抛物线的解析式为![]() ;
;
(2)①以AD为底时,AB=BD,
设直线BC的解析式为y=kx+b,则![]() ,
,
∴直线BC的解析式为y=2x2,
设D(x,2x2),由(2x2)2+(1x)2=25,解得,
∴D1 ![]() ,D2
,D2![]() ,
,
②以BD为底时,AB=AD,
B点关于AC的对称点D3(1,4),
综上所述,满足条件的D点有D1 ![]() ,D2
,D2![]() ,D3(1,4);
,D3(1,4);
∵AC2+BC2=AB2,
∴∠ACB=90°,
当P点在第三象限时,
设(2)中AD3交抛物线![]() 于P点,
于P点,
过P点作PQ⊥AC于Q点,由(2)可知∠BAC=∠PAC,
∠ACB=∠AQP, ∴△APQ∽△ABC,
设直线AP的解析式为y=mx+n,由![]() ,解得,
,解得, 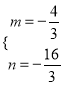

∴直线AP的解析式为![]() ,
,
由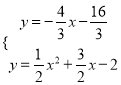 ,解得,
,解得, 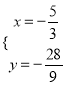 或
或![]() (舍去),
(舍去),
∴P![]() ;
;
当P点在第三象限时,
过A点作AP′⊥AD3,交抛物线![]() 于P′点,
于P′点,
过P′点作P′Q′⊥AC于Q′点,由(2)可知∠BAC=∠AP′Q′,
∠ACB=∠AQ′P′, ∴△P′AQ′∽△ABC,
易得直线AP′的解析式为![]() ,
,
同(3)过程可求P′![]() ,
,
综上,满足条件的点P有P![]() 和P′
和P′![]()
此题解法不唯一,请酌情评分.


科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
A.(x+2)2=1
B.(x﹣2)2=1
C.(x+2)2=9
D.(x﹣2)2=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .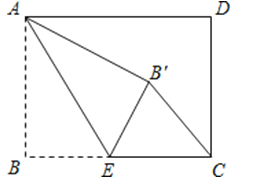
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师出了这样一道题:“已知a=2019-2,b=(-2018)3,求代数式(a-3b)2-2a(a-7b)+(a+b)(a-9b)+1的值.”小明觉得计算量太大了,请你来帮他解决,并写出具体过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
A.2015年三类农作物的产量比2014年都有增加
B.玉米产量和杂粮产量增长率相当
C.2014年杂粮产量是玉米产量的约七分之一
D.2014年和2015年的小麦产量基本持平
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记者从文化和旅游部了解到,2019年春节假期,全国旅游接待总人数415000000次数,415000000用科学记数法可表示为( )
A. 415×106B. 41.5×107C. 4.15×108D. 0.415×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②![]() AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
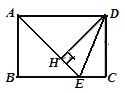
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com