练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD中，AD=AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接DE，下列结论：①∠AED=∠CED；②AED为等腰三角形；③EH=CE；④图中有3个等腰三角形.结论正确的个数为（　　）

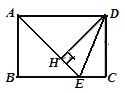
    A. 1个 B. 2个 C. 3个 D. 4个

    【答案】D

    【解析】试题分析：设AB=1，则根据角平分线的性质可得：BE=AE=1，则AE=，根据题意可得：AD=，则△AED为等腰三角形；则∠AED=∠ADE，根据平行线的性质可得：∠ADE=∠DEC，则∠AED=∠CED；根据∠AED=∠CED，∠DHE=∠C=90°，DE=DE可得：△HDE和△CDE，则EH=CE；根据题意可得：△ABE、△AHD和△ADE为等腰三角形，则题中的4个都正确.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c交x轴于A(-4，0),B（1，0),交y轴于C点，且OC=2OB.

    （1）求抛物线的解析式；

    （2）在直线BC上找点D，使△ABD为以AB为腰的等腰三角形，求D点的坐标；

    （3）在抛物线上是否存在异于B的点P，过P点作PQ⊥AC于Q，使△APQ与△ABC相似？若存在，请求出P点坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看3次的人数没有标出）．
    根据上述信息，解答下列问题：
    （1）该班级女生人数是多少？女生收看“两会”新闻次数的中位数是多少？
    （2）对于某个群体，我们把一周内收看热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体多某热点新闻的“关注指数”，如果该班级男生对“两会”新闻的“关注指数”比女生低5%，试求该班级男生人数；
    （3）为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计量，根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小．

    统计量

    平均数（次）

    中位数（次）

    众数（次）

    方差

    …

    该班级男生

    3

    3

    4

    2

    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形．已知四边形ABCD的中点四边形是正方形，对角线AC与BD的关系，下列说法正确的是（　　）

    A. AC，BD相等且互相平分B. AC，BD垂直且互相平分

    C. AC，BD相等且互相垂直D. AC，BD垂直且平分对角

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法不正确的是（ ）
    A.0.4的算术平方根是0.2
    B.﹣9是81的一个平方根
    C.﹣27的立方根是﹣3
    D.1﹣ 的相反数是 ﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】新能源汽车节能、环保，越来越受消费者喜爱，各种品牌相继投放市场，我国新能源汽车近几年销量全球第一，2016年销量为50.7万辆，销量逐年增加，到2018年销量为125.6万辆．设年平均增长率为x，可列方程为（　　）

    A. 50.7（1+x）2＝125.6B. 125.6（1﹣x）2＝50.7

    C. 50.7（1+2x）＝125.6D. 50.7（1+x2）＝125.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
    （1）求证：CE=AD；
    （2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
    （3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．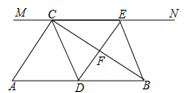

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果水位升高3m时水位变化记作+3m，那么水位下降2m时水位变化记作：m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：

    x

    …

    ﹣1

    0

    1

    2

    3

    4

    …

    y

    …

    10

    5

    2

    1

    2

    5

    …

    若A（m，y1），B（m﹣2，y2）两点都在该函数的图象上，当m=时，y1=y2 ．

    查看答案和解析>>

    同步练习册答案