
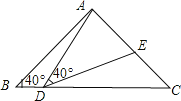
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AB£ΩAC£Ω2£¨°œB£Ω°œC£Ω40°„£¨µ„D‘⁄œþ∂ŒBC…œ‘À∂Ø£®D≤ª”ÎB°¢C÷ÿ∫œ£©£¨¡¨Ω”AD£¨◊˜°œADE£Ω40°„£¨DEΩªœþ∂ŒAC”⁄E£Æ
£®1£©µ±°œBDA£Ω115°„ ±£¨°œEDC£Ω°° °°°„£¨°œDEC£Ω°° °°°„£ªµ„D¥”BœÚC‘À∂Ø ±£¨°œBDA÷Ω•±‰°° °°£®ÃÓ°∞¥Û°±ªÚ°∞–°°±£©£ª
£®2£©µ±DCµ»”⁄∂ý…Ÿ ±£¨°˜ABD°’°˜DCE£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©‘⁄µ„Dµƒ‘À∂Øπ˝≥Ã÷–£¨°˜ADEµƒ–Œ◊¥ø…“‘ «µ»—¸»˝Ω«–Œ¬£ø»Ùø…“‘£¨«Î÷±Ω”–¥≥ˆ°œBDAµƒ∂» ˝£Æ»Ù≤ªø…“‘£¨«ÎÀµ√˜¿Ì”…£Æ

°æ¥∞∏°ø£®1£©25°„£¨115°„£¨–°£ª£®2£©µ±DC£Ω2 ±£¨°˜ABD°’°˜DCE£¨º˚Ω‚Œˆ£ª£®3£©µ±°œBDAµƒ∂» ˝Œ™110°„ªÚ80°„ ±£¨°˜ADEµƒ–Œ◊¥ «µ»—¸»˝Ω«–Œ£¨º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©∏˘æð°œBDA£Ω115°„“‘º∞°œADE£Ω40°„£¨º¥ø…µ√≥ˆ°œEDC£Ω180°„©Å°œADB©Å°œADE£¨Ω¯∂¯«Û≥ˆ°œDECµƒ∂» ˝£¨
£®2£©µ±DC£Ω2 ±£¨¿˚”√°œDEC+°œEDC£Ω140°„£¨°œADB+°œEDC£Ω140°„£¨«Û≥ˆ°œADB£Ω°œDEC£¨‘Ÿ¿˚”√AB£ΩDC£Ω2£¨º¥ø…µ√≥ˆ°˜ABD°’°˜DCE£¨
£®3£©µ±°œBDAµƒ∂» ˝Œ™110°„ªÚ80°„ ±£¨°˜ADEµƒ–Œ◊¥ «µ»—¸»˝Ω«–Œ£Æ
Ω‚£∫£®1£©°œEDC£Ω180°„©Å°œADB©Å°œADE£Ω180°„©Å115°„©Å40°„£Ω25°„£¨
°œDEC£Ω180°„©Å°œEDC©Å°œC£Ω180°„©Å40°„©Å25°„£Ω115°„£¨
°œBDA÷Ω•±‰–°£ª
π ¥∞∏Œ™£∫25°„£¨115°„£¨–°£ª
£®2£©µ±DC£Ω2 ±£¨°˜ABD°’°˜DCE£¨
¿Ì”…£∫°þ°œC£Ω40°„£¨
°ý°œDEC+°œEDC£Ω140°„£¨
”÷°þ°œADE£Ω40°„£¨
°ý°œADB+°œEDC£Ω140°„£¨
°ý°œADB£Ω°œDEC£¨
”÷°þAB£ΩDC£Ω2£¨
°ý°˜ABD°’°˜DCE£®AAS£©£¨
£®3£©µ±°œBDAµƒ∂» ˝Œ™110°„ªÚ80°„ ±£¨°˜ADEµƒ–Œ◊¥ «µ»—¸»˝Ω«–Œ£¨
¿Ì”…£∫°þ°œBDA£Ω110°„ ±£¨
°ý°œADC£Ω70°„£¨
°þ°œC£Ω40°„£¨
°ý°œDAC£Ω70°„£¨°œAED£Ω°œC+°œEDC£Ω30°„+40°„£Ω70°„£¨
°ý°œDAC£Ω°œAED£¨
°ý°˜ADEµƒ–Œ◊¥ «µ»—¸»˝Ω«–Œ£ª
°þµ±°œBDAµƒ∂» ˝Œ™80°„ ±£¨
°ý°œADC£Ω100°„£¨
°þ°œC£Ω40°„£¨
°ý°œDAC£Ω40°„£¨
°ý°œDAC£Ω°œADE£¨
°ý°˜ADEµƒ–Œ◊¥ «µ»—¸»˝Ω«–Œ£Æ


 ±∏’Ω÷–øº∫ƺŸœµ¡–¥∞∏
±∏’Ω÷–øº∫ƺŸœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AD «BC±þ…œµƒ÷–œþ£¨E «ADµƒ÷–µ„£¨π˝µ„A◊˜BCµƒ∆Ω––œþΩªBEµƒ—”≥§œþ”⁄µ„F£¨¡¨Ω”CF£Æ

£®1£©«Û÷§£∫AF=DC£ª
£®2£©»ÙAB°ÕAC£¨ ‘≈–∂œÀƒ±þ–ŒADCFµƒ–Œ◊¥£¨≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ƒ≥µÁƒ‘π´Àæœ÷”–A£¨B£¨C»˝÷÷–Õ∫≈µƒº◊∆∑≈∆µÁƒ‘∫ÕD£¨E¡Ω÷÷–Õ∫≈µƒ““∆∑≈∆µÁƒ‘.œ£Õ˚÷–—ß“™¥”º◊°¢““¡Ω÷÷∆∑≈∆µÁƒ‘÷–∏˜—°π∫“ª÷÷–Õ∫≈µƒµÁƒ‘.
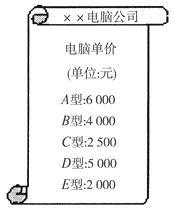
(1)–¥≥ˆÀ˘”–—°π∫∑Ω∞∏(¿˚”√ ˜◊¥ÕºªÚ¡–±Ì∑Ω∑®±Ì 棩£ª
(2)»Áπ˚(1)÷–∏˜÷÷—°π∫∑Ω∞∏±ª—°÷–µƒø…ƒÐ–‘œýÕ¨£¨ƒ«√¥A–Õ∫≈µÁƒ‘±ª—°÷–µƒ∏≈¬ «∂ý…Ÿ£ø
(3)œ÷÷™œ£Õ˚÷–—ß”√10ÕÚ‘™π∫¬Úº◊°¢““¡Ω÷÷∆∑≈∆µÁƒ‘π≤36î(º€∏Ò»ÁÕºÀ˘ æ)£¨∆‰÷–º◊∆∑≈∆µÁƒ‘Œ™A–Õ∫≈µÁƒ‘£¨«Ûπ∫¬ÚµƒA–Õ∫≈µÁƒ‘”–∂ý…ŸÃ®£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™‘⁄µ»—¸»˝Ω«–ŒABC÷–£¨AB=AC£¨BD°ÕAC”⁄µ„D£¨CE°ÕAB”⁄µ„E£¨CE”ÎBDΩª”⁄µ„O.

(1)«Û÷§£∫°˜BCE°’°˜CBD£ª
(2)–¥≥ˆÕº÷–À˘”–œýµ»µƒœþ∂Œ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨DŒ™µ»±þ°˜ABC±þBC…œ“ªµ„£¨DE°ÕAB”⁄E£¨»ÙBD£∫CD=2£∫1£¨DE=2![]() £¨ «ÛAE£Æ
£¨ «ÛAE£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
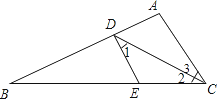
°æƒø°ø»ÁÕº£¨“—÷™CD∆Ω∑÷°œACB£¨°œ1=°œ2£Æ
£®1£©«Û÷§£∫DE°ŒAC£ª
£®2£©»Ù°œ3=30°„£¨°œB=25°„£¨«Û°œBDEµƒ∂» ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄◊€∫œ µº˘øŒ…œ£¨–°¥œÀ˘‘⁄–°◊È“™≤‚¡ø“ªÃı∫”µƒøÌ∂»£¨»ÁÕº£¨∫”∞∂EF°ŒMN£¨–°¥œ‘⁄∫”∞∂MN…œµ„A¥¶”√≤‚«„∆˜≤‚µ√∫”∂‘∞∂–° ˜CŒª”⁄∂´±±∑ΩœÚ£¨»ª∫Û—ÿ∫”∞∂◊þ¡À30√◊£¨µΩ¥ÔB¥¶£¨≤‚µ√∫”∂‘∞∂µÁœþ∏ÀDŒª”⁄±±∆´∂´30°„∑ΩœÚ£¨¥À ±£¨∆‰À˚Õ¨—ß≤‚µ√CD£Ω10√◊£Æ‘Ú∫”µƒøÌ∂»Œ™________√◊(Ω·π˚±£¡Ù∏˘∫≈).

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™µ»—¸»˝Ω«–Œµƒ“ª±þ≥§Œ™2£¨÷Ð≥§Œ™8£¨ƒ«√¥À¸µƒ—¸≥§Œ™ ( )
A. 2 B. 3 C. 2ªÚ3 D. ≤ªƒÐ»∑∂®
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„A°¢ Bµƒ◊¯±Í∑÷±Œ™£®0£¨2£©£¨£®1£¨0£©£¨÷±œþy=![]() x3”Îy÷·Ωª”⁄µ„C£¨ ”Îx÷·Ωª”⁄µ„D£¨
x3”Îy÷·Ωª”⁄µ„C£¨ ”Îx÷·Ωª”⁄µ„D£¨

£®1£©«Û÷±œþAB”ÎCDΩªµ„Eµƒ◊¯±Í£ª
£®2£©«ÛÀƒ±þ–ŒOBECµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com