【题目】（本题8分）如图某幢大楼顶部有广告牌CD．张老师目高MA为1.60米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进14米、站在点B处，测得广告牌顶端点C的仰角为45°．（取
,计算结果保留一位小数）
（1）求这幢大楼的高DH；
（2）求这块广告牌CD的高度．
【答案】（1）27.6米；(2) 5.0米
【解析】试题分析：首先分析图形：根据题意构造直角三角形Rt△DME与Rt△CNE；应利用ME﹣NE=AB=14构造方程关系式，进而可解即可求出答案．
试题解析：解：（1）在Rt△DME中，ME=AH=45米；
由tan30°=
，得DE=45×
=15×1.732=25.98米；
又因为EH=MA=1.6米，因而大楼DH=DE+EH=25.98+1.6=27.58≈27.6米；
（2）又在Rt△CNE中，NE=45﹣14=31米，由tan45°=
，得CE=NE=31米；
因而广告牌CD=CE﹣DE=31﹣25.98≈5.0米；
答：楼高DH为27.6米，广告牌CD的高度为5.0米．
科目：初中数学 来源： 题型：
【题目】要了解全校学生的课外作业负担情况，以下抽样方法中比较合理的是（ ）
A.调查全体女生的作业B.调查全体男生的作业
C.调查九年级全体学生的作业D.调查七、八、九年级各 100 名学生 的作业
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于实数a，我们规定：用符号
表示不大于
的最大整数，称
为a的根整数，例如： 
， 
．
（1）仿照以上方法计算： 
= ； 
= ．
（2）若
=1，写出满足题意的x的整数值 ．
如果我们对a连续求根整数，直到结果为1为止．例如：对10连续求根整数2次 
，这时候结果为1．
（3）对100连续求根整数， 次之后结果为1．
（4）只需进行3次连续求根整数运算后结果为1的所有正整数中，最大的是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，边长为6的正方形OABC的顶点A，C分别在x轴和y轴的正半轴上，直线y=mx+2与OC，BC两边分别相交于点D，G，以DG为边作菱形DEFG，顶点E在OA边上．
（1）如图1，顶点F在边AB上，当CG=OD时，
求m的值；
菱形DEFG是正方形吗?如果是请给予证明.
（2）如图2，连接BF，设CG=a，△FBG的面积为S，求S与a的函数关系式；
（3）如图3，连接GE，当GD平分∠CGE时，请直接写出m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
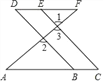
【题目】已知：如图，∠1=∠2，∠A=∠F，试说明∠C=∠D．
解：∵∠1=∠2 （已知 ）
∠1=∠ （ ）
∴∠2=∠ （等量代换）
∴BD∥ （ ）
∴∠ABD=∠ （两直线平行，同位角相等）
∵∠A=∠F （ 已知 ）
∴DF∥ （ ）
∴∠ABD=∠ （两直线平行，内错角相等）
∴∠C=∠D （ ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y=a（x﹣4）2+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．
（1）当a=﹣
时，①求h的值；②通过计算判断此球能否过网．
（2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为
m的Q处时，乙扣球成功，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题6分）甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．
（1）甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；
（2）若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．
查看答案和解析>>
科目：初中数学 来源： 题型：
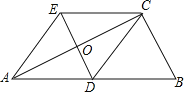
【题目】在ABC中，∠BCA=90°，CD是边AB上的中线，分别过点C，D作BA，BC的平行线交于点E，且DE交AC于点O，连接AE.
(1)求证：四边形ADCE是菱形；
(2)若AC=2DE，求sin∠CDB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com