
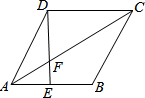
 如图,?ABCD中,AE:EB=2:3,DE交AC于F.
如图,?ABCD中,AE:EB=2:3,DE交AC于F. 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,| △AEF的周长 |
| △CDF的周长 |
| AE |
| DC |
| 2λ |
| 5λ |
| S△CDF |
| S△AEF |
| CD |
| AE |
| CD |
| AE |
| 5λ |
| 2λ |
| 5 |
| 2 |
| 16 |
| 5 |


科目:初中数学 来源: 题型:
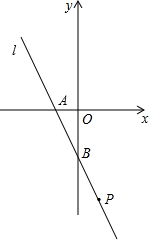 如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足
如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足| OA-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
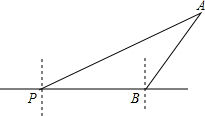 如图,一艘轮船位于P时测得灯塔A在其北偏东60°方向,它沿着正东方向行驶400海里到达B处,此时测得灯塔A在其北偏东30°方向,已知以灯塔A为圆心,300海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁的危险.
如图,一艘轮船位于P时测得灯塔A在其北偏东60°方向,它沿着正东方向行驶400海里到达B处,此时测得灯塔A在其北偏东30°方向,已知以灯塔A为圆心,300海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁的危险.查看答案和解析>>
科目:初中数学 来源: 题型:
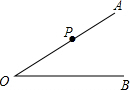 如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)
如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:
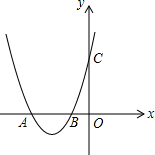 已知:如图,抛物线C1:y=ax2+4ax+c的图象开口向上,与x轴交于点A、B(A在B的左边),与y轴交于点C,顶点为P,AB=2,且OA=OC.
已知:如图,抛物线C1:y=ax2+4ax+c的图象开口向上,与x轴交于点A、B(A在B的左边),与y轴交于点C,顶点为P,AB=2,且OA=OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com