练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,直线a,b被直线c所截．若a∥b,∠1=60°，则∠2= ___ ____度．

     



    120


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     观察下面的表格．

    0

    1

    2

    1

    -3

    -3

    （1）       求a、b、c的值

    （2）       设y＝ax2＋bx＋c，求这个二次函数图象的对称轴和图象与x轴的交点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知x1、x2是方程x2－（k－2）x＋k2＋3k＋5＝0的两个实数根，则＋的最大值是

    A．13          B．18          C．15           D．19

    查看答案和解析>>

    科目：初中数学 来源： 题型：


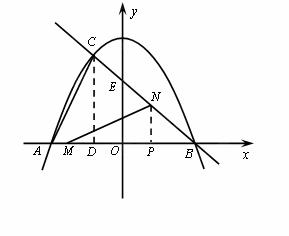
    如图，抛物线y＝－x 2＋3与x轴交于点A、点B，与直线y＝－x ＋b相交于点B、点C，直线y＝－x ＋b与y轴交于点E．

    （1）求直线BC的解析式．

    （2）求△ABC的面积．

    （3）若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A、B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动．设运动时间为t秒，请写出△MNB的面积S与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    圆锥的母线为6cm，底面半径为2cm，则圆锥的高为（　 　）

        A．cm           B．3cm         

    C．4cm          D． 4cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    图1是边长分别为4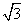和2的两个等边三角形纸片ABC和ODE叠放在一起（C与O重合）.

    （1）操作：固定△ABC，将△0DE绕点C顺时针旋转30°后得到△ODE，连结AD、BE，CE的延长线交AB于F（图2）；

    探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论.

    （2）在（1）的条件下将的△ODE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR，当点P与点F重合时停止运动（图3）

    探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围.

    （3）将图1中△0DE固定，把△ABC沿着OE方向平移，使顶点C落在OE的中点G处，设为△ABG，然后将△ABG绕点G顺时针旋转，边BG交边DE于点M，边AG交边DO于点N，设∠BGE=α（30°＜α＜90°）；(图4)

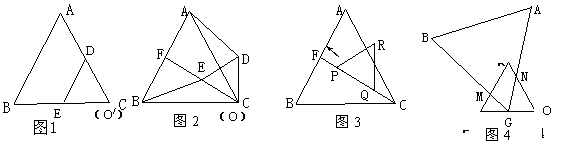    探究：在图4中，线段ON·EM的值是否随α的变化而变化？如果没有变化，请你

    求出ON·EM的值，如果有变化，请你说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AC的垂直平分线ED交AC于点E，交 AB于点D，CE=4，△BCD的周长等于18，则△ABC的周长为　       　.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝，点E，F，G，H分别是四边形ABCD各边的中点.其中阴影部分用甲布料，其余部分用乙布料（裁剪两种布料时，均 不计余料）.若生产这批风筝需要甲布料30匹，那么需要乙布料

    A．15匹        B．30匹      C．60匹       D．30匹

     


    查看答案和解析>>

    同步练习册答案