
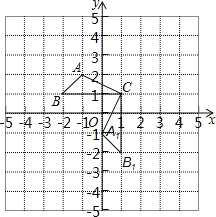
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点__逆时针旋转__度得到的,B1的坐标是__;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列式子:(1)4>0;(2)2x+3y<0;(3)x=3;(4)x≠y;(5)x+y;(6)x+3≤7中,不等式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名学生所捐款的数额,下列说法正确的是( )
A.众数是100
B.平均数是30
C.极差是20
D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
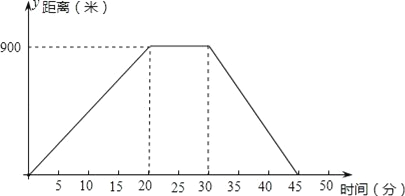
【题目】如图所示,是反映了爷爷每天晚饭或从家中出发去散步的时间与距离之间的关系的一幅图.
(1)下图反映了哪两个变量之间的关系?
(2)爷爷从家里出发后20分钟到30分钟可能在做什么?
(3)爷爷每天散步多长时间?
(4)爷爷散步时最远离家多少米?
(5)计算爷爷离开家后的20分钟内的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
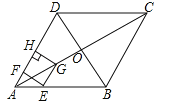
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为 ;当OO′⊥AD时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 4 | 2 | 5 | 1 |
这此测试成绩的中位数和众数分别为( )
A.47,49
B.47.5,49
C.48,49
D.48,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】对于任意正实数a、b,
∵(![]() -
-![]() )2≥0,∴a-2
)2≥0,∴a-2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
【获得结论】在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:(1)若![]() >0,只有当
>0,只有当![]() = 时,m+
= 时,m+![]() 有最小值 .
有最小值 .
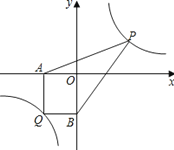
【探索应用】(2)已知点Q(-3,-4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com