
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=8����BAD=60�㣬��E�ӵ�A��������AB��ÿ��2����λ���ȵ��ٶ����յ�B�˶�������E�����A�غ�ʱ������E��EF��AD�ڵ�F����EG��AD��AC�ڵ�G������G��GH��AD��AD����AD���ӳ��ߣ��ڵ�H���õ�����EFHG�����E�˶���ʱ��Ϊt��
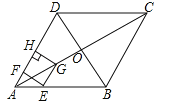
��1�����߶�EF�ij����ú�t�Ĵ���ʽ��ʾ����
��2�����H���D�غ�ʱt��ֵ��
��3�������EFHG������ABCD�ص�����ͼ�ε������Sƽ����λ����S��t֮��ĺ�����ϵʽ��
��4������EFHG�ĶԽ���EH��FG�ཻ�ڵ�O�䣬��OO���ADʱ��t��ֵΪ ����OO���ADʱ��t��ֵΪ ��
���𰸡���1��EF=![]() t����2��t=
t����2��t=![]() ����3��
����3��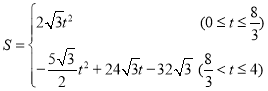 ����4��t=4��t=3��
����4��t=4��t=3��
��������
�����������1��������֪��AE=2t����������Ǻ������ɵó�EF=![]() t��
t��
��2����H��D�غ�ʱ��FH=GH=8��t�������ε����ʺ�EG��AD��֪��AE=EG�����t=![]() ��
��
��3������EFHG������ABCD�ص�����ͼ����Ҫ����������������ۣ��ٵ�H���߶�AD�ϣ���ʱ�غϵIJ���Ϊ����EFHG���ڵ�H���߶�AD���ӳ�����ʱ���غϵIJ���Ϊ����Σ�
��4����OO���ADʱ����ʱ��E��B�غϣ���OO���ADʱ������O��OM��AD�ڵ�M��EF��OA�ཻ�ڵ�N��Ȼ��ֱ����O��M��O��F��FM�����ù��ɶ����г����̼������t��ֵ��
�����������1��������֪��AE=2t��0��t��4���ߡ�BAD=60�㣬��AFE=90�㣬��sin��BAD=![]() ����EF=
����EF=![]() t��
t��
��2����AE=2t����AEF=30�㣬��AF=t����H��D�غ�ʱ����ʱFH=8��t����GE=8��t����EG��AD�����EGA=30�㣬���ı���ABCD�����Σ����BAC=30�㣬���BAC=��EGA=30�㣬��AE=EG����2t=8��t����t=![]() ��
��
��3����0��t��![]() ʱ����ʱ����EFHG������ABCD�ص�����ͼ��Ϊ����EFHG�����ɣ�2����֪��AE=EG=2t����S=EFEG=
ʱ����ʱ����EFHG������ABCD�ص�����ͼ��Ϊ����EFHG�����ɣ�2����֪��AE=EG=2t����S=EFEG=![]() t2t=
t2t=![]() ��
��
��![]() ��t��4ʱ����ͼ1����CD��HG���ڵ�I����ʱ����EFHG������ABCD�ص�����ͼ��Ϊ�����FEGID����AE=2t����AF=t��EF=
��t��4ʱ����ͼ1����CD��HG���ڵ�I����ʱ����EFHG������ABCD�ص�����ͼ��Ϊ�����FEGID����AE=2t����AF=t��EF=![]() t����DF=8��t����AE=EG=FH=2t����DH=2t����8��t��=3t��8���ߡ�HDI=��BAD=60�㣬��tan��HDI=
t����DF=8��t����AE=EG=FH=2t����DH=2t����8��t��=3t��8���ߡ�HDI=��BAD=60�㣬��tan��HDI=![]() ����HI=
����HI=![]() DH����S=EFEG��
DH����S=EFEG��![]() DHHI=
DHHI=![]() =
=![]() ��
��
����������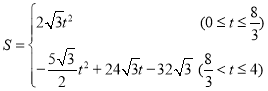 ��
��
��4����OO���ADʱ����ͼ2����ʱ��E��B�غϣ���t=4��
��OO���ADʱ����ͼ3������O��OM��AD�ڵ�M��EF��OA�ཻ�ڵ�N���ɣ�2����֪��AF=t��AE=EG=2t����FN=![]() t��FM=t����O��O��AD��O����FG���е㣬��O��O�ǡ�FNG����λ�ߣ���O��O=
t��FM=t����O��O��AD��O����FG���е㣬��O��O�ǡ�FNG����λ�ߣ���O��O=![]() FN=
FN=![]() t����AB=8�����ɹ��ɶ�������ã�OA=
t����AB=8�����ɹ��ɶ�������ã�OA=![]() ����OM=
����OM=![]() ����O��M=
����O��M=![]() ����FE=
����FE=![]() t��EG=2t�����ɹ��ɶ�������ã�
t��EG=2t�����ɹ��ɶ�������ã�![]() �����ɾ��ε����ʿ�֪��
�����ɾ��ε����ʿ�֪��![]() �����ɹ��ɶ�����֪��
�����ɹ��ɶ�����֪��![]() ����
����![]() ����t=3��t=��6����ȥ����
����t=3��t=��6����ȥ����
�ʴ�Ϊ��t=4��t=3��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˺��ᆪ�����㴫ͳ�Ļ���ij��ѧ�ٰ��˾����Ļ�֪ʶ������������ǣ�ÿλ����ѡ�ֻش�100��ѡ���⣬���һ���1�֣��������÷֡����۷֣������ȫ�����ѡ�ֵĴ���������������ͳ�ƣ����������Ƴ�����ͼ����
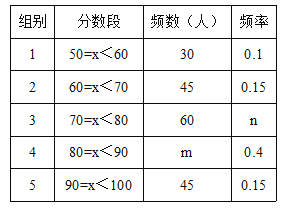
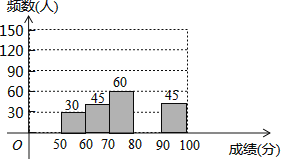
�������ͼ����Ϣ������������⣺
��1������m=������n=������
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��ȫ�����ѡ�ֳɼ�����λ�����ڵڼ��飻
��4�����÷���80�����ϣ���80�֣���ѡ�ֿɻ����ߴ����в���ѡ��������ɷ�1�ˣ�������ѡ��ǡ���ǻ��ߵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��дһ��������ϵ��Ϊ1��һԪ���η��̣�ʹ�������ֱ���-2��1. _______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA����1��2����B����2��1����C��1��1����������������ÿ��С�����εı߳���1����λ���ȣ���
��1����A1B1C1�ǡ�ABC�Ƶ�__��ʱ����ת__�ȵõ��ģ�B1��������__��
��2������߶�AC��ת��������ɨ�����������������У���
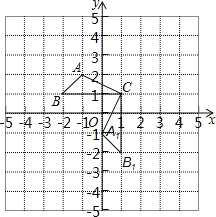
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������������С���Ļ����м�һ������6����3��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬ������ͷ��8ֻ��������26ֻ��������________ֻ����________ֻ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������x��һԪ���η���x2+bx+1=0����b��0ʱ����ʵ����������˵����������Ǽ������һ�����������ǣ� ��
A. b=��1 B. b=2 C. b=��2 D. b=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ����( )
A. �ı߶���ȵ��ı�����ƽ���ı���
B. ����ԽǷֱ���ȵ��ı�����ƽ���ı���
C. �Խ����ഹֱ���ı�����ƽ���ı���
D. ����Ա߷ֱ�ƽ�е��ı�����ƽ���ı���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com