Question

周长是94、各边长都是整数的各个矩形中，最大的面积是________．

Answer 1

552
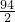
分析：先设矩形的长是x，宽是（-x），则S=-x²+47x，由于a=-1＜0，则说明S有最大值，而矩形的各边长都是整数，易求出x的值，进而可求宽，从而可求面积．
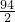
解答：设矩形的长是x，宽是（-x），则
S=x（47-x）=-x²+47x，
∵a=-1＜0，
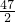
∴当x=-==23.5时，S有最大值，
又∵x是整数，
∴当x=24，47-x=23时，
∴S_最大值=23×24=552．
故答案是552．
点评：本题考查了有理数的最值，解题的关键是注意矩形的各边长都是整数的条件．