
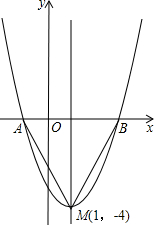
 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).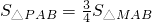 ?若存在,求出P点的坐标;若不存在,请说明理由;
?若存在,求出P点的坐标;若不存在,请说明理由; S△MAB,
S△MAB, AB•h=
AB•h= •
• AB•4,
AB•4,
 +1,x2=-
+1,x2=- +1,
+1, +1,3)或(-
+1,3)或(- +1,3),
+1,3), +1,3),(-
+1,3),(- +1,3);
+1,3); ,
, ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
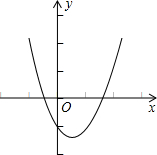 如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①c>0;②a+b+c<0;③2a-b<0;④b2+8a>4ac中正确的是(填写序号)
如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①c>0;②a+b+c<0;③2a-b<0;④b2+8a>4ac中正确的是(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com