
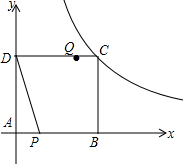
 ��֪������ABCD������A������ԭ���غϣ�����B��D�ֱ���x���y����������ϣ�����C�ڷ���������y=$\frac{16}{x}$��x��0����ͼ���ϣ���ͼ��ʾ������P��ÿ��1����λ���ٶȴ�A�������AB�����˶�������Qͬʱ��ÿ��4����λ�ٶȴ�D������������εı�DC-CB-BA����˳ʱ�������˶�������P���Q����ʱֹͣ�˶������P���˶�ʱ��Ϊt��
��֪������ABCD������A������ԭ���غϣ�����B��D�ֱ���x���y����������ϣ�����C�ڷ���������y=$\frac{16}{x}$��x��0����ͼ���ϣ���ͼ��ʾ������P��ÿ��1����λ���ٶȴ�A�������AB�����˶�������Qͬʱ��ÿ��4����λ�ٶȴ�D������������εı�DC-CB-BA����˳ʱ�������˶�������P���Q����ʱֹͣ�˶������P���˶�ʱ��Ϊt������ ��1�����C������Ϊ��a��a����������뷴������������ʽ���ɵõ�a=4��
��2���ֵ�Q��CD��BC��AB���ϣ��������������ʽ�����ͼ�ε�������㼴����⣻
��3���ֵ�Q��CD��BC��AB���ϣ�����ȫ�������ε��ж���������õ�Q�����꣮
��� �⣺��1�����C������Ϊ��a��a����a��0������
a=$\frac{16}{a}$��
���a=4��
����C�������ǣ�4��4����
���������εı߳�Ϊ4��
��2����0��t��1ʱ��Q��DC�ϣ�DQ=4t����S=$\frac{1}{2}$��4t��4=8t��
��1��t��2ʱ��Q��BC�ϣ���BP=4-t��CQ=4t-4��AP=t��
��S=S������ABCD-S��APD-S��BPQ-S��CDQ=16-$\frac{1}{2}$AP•AD-$\frac{1}{2}$PB•BQ-$\frac{1}{2}$DC•CQ=16-$\frac{1}{2}$t��4-$\frac{1}{2}$��4-t��•[4-��4t-4��]-$\frac{1}{2}$��4��4t-4��=-2t2+2t+8��
��2��t��$\frac{12}{5}$ʱ��Q��AB�ϣ�PQ=12-5t����s=$\frac{1}{2}$��4����12-5t������S=-10t+24��
��֮��S=$\left\{\begin{array}{l}{8t��0��t��1��}\\{-2t2+2t+8��1��t��2��}\\{-10t+24��2��t��\frac{12}{5}��}\end{array}\right.$��
��3����Q��DC��ʱ����ͼ��ʾ��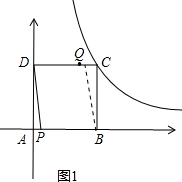
��ʱ��APD�ա�CQB��
��AP=CQ����t=4-4t�����t=$\frac{4}{5}$��
��DQ=4t=$\frac{16}{5}$����Q1��$\frac{16}{5}$��4����
��Q��BC����ʱ��������λ�ã���ͼ��ʾ��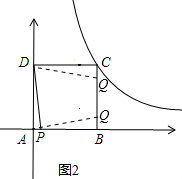
��Q���ϱߣ����QCD�ա�PAD��
��AP=QC����4t-4=t�����t=$\frac{4}{3}$��
��QB=8-4t=$\frac{8}{3}$����ʱQ2��4��$\frac{8}{3}$����
��Q���±ߣ����APD�ա�BQA��
��AP=BQ����8-4t=t�����t=$\frac{8}{5}$��
��QB=$\frac{8}{5}$����Q3��4��$\frac{8}{5}$����
��Q��AB����ʱ����ͼ��ʾ��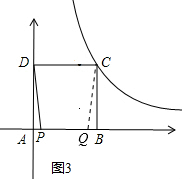
��ʱ��APD�ա�QBC��
��AP=BQ����4t-8=t�����t=$\frac{8}{3}$��
��Ϊ0��t��$\frac{12}{5}$������t=$\frac{8}{3}$�������⣬��ȥ��
��������Q1��$\frac{16}{5}$��4���� Q2��4��$\frac{8}{3}$����Q3��4��$\frac{8}{5}$����
���� ���⿼���������ε����ʣ�����ϵ����������������ʽ��ȫ�������ε��ж������ʣ������ε�������㣮����ʱҪ�Ե�Q�IJ�ͬλ�ý��з������ۣ��Է�©�⣬�����ۺ��Խ�ǿ����һ�����Ѷȣ�


 Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
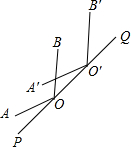 ��ͼ����O��ֱ��PQ�ϣ���AOP=20�㣬����AOB��PQ����ƽ��һ�ξ����õ���A��O��B�䣬���С�B��O��Q=40�㣬���AOB�Ķ���Ϊ��������
��ͼ����O��ֱ��PQ�ϣ���AOP=20�㣬����AOB��PQ����ƽ��һ�ξ����õ���A��O��B�䣬���С�B��O��Q=40�㣬���AOB�Ķ���Ϊ��������| A�� | 120�� | B�� | 140�� | C�� | 150�� | D�� | 160�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | 9 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
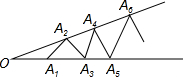 ��ͼ����֪��A1��A2��A3��A4���ǡ�O�����ϵĵ㣬��O A1=A1 A2=A2 A3=A3 A4=A4 A5=����������������ǡ��ֻ������4�����������Σ����ʡ�O=18�㣮
��ͼ����֪��A1��A2��A3��A4���ǡ�O�����ϵĵ㣬��O A1=A1 A2=A2 A3=A3 A4=A4 A5=����������������ǡ��ֻ������4�����������Σ����ʡ�O=18�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{{x}^{2}}$-1=��$\frac{1}{x}$+1����$\frac{1}{x}$-1�� | B�� | ��a+b��2=a2+2ab+b2 | C�� | x2-x-2=��x+1����x-2�� | D�� | ax-ay-a=a��x-y��-1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com