
如图七,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N分别为线段AC和
射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.
(1)求证:MN∶NP为定值;
(2)若△BNP与△MNA相似,求CM的长;
(3)若△BNP是等腰三角形,求CM的长.
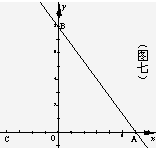
证明:(1) 过点N作NH⊥x轴于点H,…………………1分
设AN=5k,得:AH=3k,CM=2k
① 当点M在CO上时,点N在线段AB上时:
∴OH=6-3k,OM=4-2k, ∴MH=10-5k,
∵PO∥NH,∴![]() ………………2分
………………2分
② 当点M在OA上时,点N在线段AB的延长线上时:
∴OH=3k-6,OM=2k-4,∴MH=5k-10,
∵PO∥NH∴,![]() ………………2分
………………2分

解:(2) 当△BNP与△MNA相似时:
① 当点M在CO上时,只可能是∠MNB=∠MNA=90°,
 ∴△BNP∽△MNA△∽BOA,
∴△BNP∽△MNA△∽BOA,
![]() ,
,![]() ,
,![]() ,
,![]() ……2分
……2分
② 当点M在OA上时,只可能是∠NBP=∠NMA,∴∠PBA=∠PMO,
∵
∴![]() ,矛盾∴不成立. ………………………2分
,矛盾∴不成立. ………………………2分
(3) ∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
① 当点M在CO上时,![]() ,
,
(ⅰ) ![]() ,
,![]() ,
,![]() ,
,![]() ………………………1分
………………………1分
(ⅱ) ![]() ,则
,则![]() ,∵
,∵![]() ,矛盾∴不成立…1分
,矛盾∴不成立…1分
(ⅲ) ![]() ,则
,则![]()
∵![]() ,
, ![]() ,∴
,∴![]()
又∵![]() ,可证△
,可证△![]() 为等腰三角形,
为等腰三角形,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ……………………………1分
……………………………1分
② 当点M在OA上时,![]() ,
,
(ⅰ) ![]() ,
,![]() ,
,![]() ,
, ![]() ………………………1分
………………………1分
(ⅱ) ![]() 或
或![]() ∵
∵![]() ,∴不成立.
,∴不成立.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC在坐标平面内三顶点的坐标分别为A(1,2)、B(3,3)、C(3,1).
如图,△ABC在坐标平面内三顶点的坐标分别为A(1,2)、B(3,3)、C(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com