练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，若AC=2，AB=3，那么cos∠BCD的值为
     
    ．
    考点：锐角三角函数的定义
    专题：
    分析：首先利用勾股定理计算出BC长，然后再利用直角三角形的面积公式计算出CD长，再用余弦定义可得答案．
    解答：解：∵AC=2，AB=3，∠ACB=90°，
    ∴BC=
    		32-22
    =
    		5
    ，
    ∵
    1
    2
    AB•CD=
    1
    2
    AC•BC，
    ∴3CD=2
    		5
    ，
    CD=
    2
    		5
    3
    ，
    ∴cos∠BCD=
    DC
    BC
    =
    2
    		5
    3
    		5
    =
    2
    3
    ，
    故答案为：
    2
    3
    ．
    点评：此题主要考查了锐角三角函数的定义，以及勾股定理的应用，关键是掌握余弦=
    邻边
    斜边
    ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知二次函数y=ax2+bx+c的图象的顶点为M（2，1），且过点N（3，2）．
    （1）求这个二次函数的关系式；
    （2）若一次函数y=-
    4
    3
    x-4的图象与x轴交于点A，与y轴交于点B，P为抛物线上的一个动点，过点P作PQ∥y轴交直线AB于点Q，以PQ为直径作圆交直线AB于点D．设点P的横坐标为n，问：当n为何值时，线段DQ的长取得最小值？最小值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系xOy（如图）中，已知：点A（3，0）、B（-2，5）、C（0，-3）．
    （1）求经过点A、B、C的抛物线的表达式；
    （2）若点D是（1）中求出的抛物线的顶点，求tan∠CAD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：-1+|-2|=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

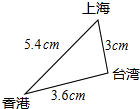    在中国地图册上，联结上海、香港、台湾三地构成一个三角形，用刻度尺测得它们之间的距离如图所示．飞机从台湾直飞上海的距离约为l290千米，那么飞机从台湾绕道香港再到上海的空中飞行距离是
     
    千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    河堤横截面如图所示，堤高BC为4米，迎水坡AB的坡比为1：
    		3
    ，那么AB的长为
     
    米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在一个边长为4cm正方形里作一个扇形（如图所示），再将这个扇形剪下卷成一个圆锥的侧面，则这个圆锥的高为
     
    cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平行四边形、矩形、等边三角形、正方形四种图形中，既是轴对称图形又是中心对称图形的有（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    合并同类项：5x2-7xy+3x2+6xy-4x2．

    查看答案和解析>>

    同步练习册答案