
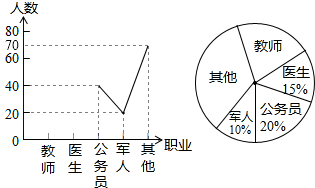
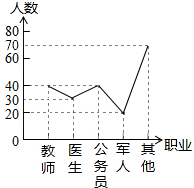
 解:(1)∵军人的人数为20,百分比为10%,
解:(1)∵军人的人数为20,百分比为10%,| 40 |
| 200 |
| 1 |
| 5 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
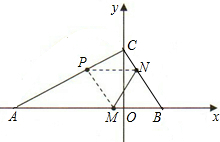 如图,已知A(-3,0),C(0,
如图,已知A(-3,0),C(0,| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
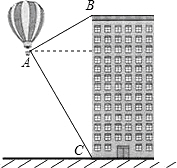 热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球A处与高楼的水平距离为120m,这栋高楼有多高(
热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球A处与高楼的水平距离为120m,这栋高楼有多高(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
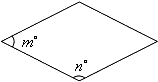 如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.
如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com