
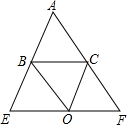
 已知,如图∠EBC与∠FCB的角平分线交于O点,过O作EF∥BC交AB延长线E点,交AC延长线于F点,∠ABC:∠ACB=3:2,
已知,如图∠EBC与∠FCB的角平分线交于O点,过O作EF∥BC交AB延长线E点,交AC延长线于F点,∠ABC:∠ACB=3:2,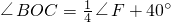 ,求∠OBC的度数.
,求∠OBC的度数. (180°-3x°),∠BCO=
(180°-3x°),∠BCO= (180°-2x°),
(180°-2x°), (180°-3x°)-
(180°-3x°)- (180°-2x°),
(180°-2x°), ∠F+40°=
∠F+40°= ×2x°+40°=
×2x°+40°= x°+40°,
x°+40°, (180°-3x°)-
(180°-3x°)- (180°-2x°)=
(180°-2x°)= x°+40°,
x°+40°, (180°-3x°)=60°.
(180°-3x°)=60°. ∠F+40°,即可列方程求解.
∠F+40°,即可列方程求解.

 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
 29、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.(1)在不添辅助线的情况下,请写出由已知条件可得出的结论(例如,可得出△ABE≌△ACD,∠DOB=∠EOC,∠DOE=∠BOC等.你写出的结论中不能含所举之例,只要求写出4个).①
29、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.(1)在不添辅助线的情况下,请写出由已知条件可得出的结论(例如,可得出△ABE≌△ACD,∠DOB=∠EOC,∠DOE=∠BOC等.你写出的结论中不能含所举之例,只要求写出4个).①查看答案和解析>>
科目:初中数学 来源: 题型:
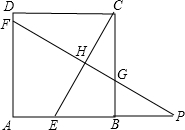 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P.| 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
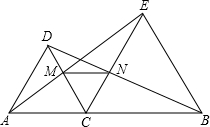 BD分别与CD、CE交于点M、N.求证:
BD分别与CD、CE交于点M、N.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图∠EBC与∠FCB的角平分线交于O点,过O作EF∥BC交AB延长线E点,交AC延长线于F点,∠ABC:∠ACB=3:2,∠BOC=
已知,如图∠EBC与∠FCB的角平分线交于O点,过O作EF∥BC交AB延长线E点,交AC延长线于F点,∠ABC:∠ACB=3:2,∠BOC=| 1 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com