
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
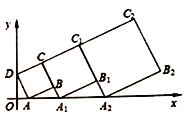
,作正方形![]() ……按这样的规律进行下去,第1个正方形的面积为_____;第4个正方形的面积为____.
……按这样的规律进行下去,第1个正方形的面积为_____;第4个正方形的面积为____.
【答案】5; ![]()
【解析】
由点A的坐标为(1,0),点D的坐标为(0,2).即可求得OA与OD的长,然后由勾股定理即可求得AD的长,继而求得第1个正方形ABCD的面积;先证得△DOA∽△ABA1,然后由相似三角形的对应边成比例,可求得A1B的长,即可求得A1C的长,即可得第2个正方形A1B1C1C的面积;以此类推,可得第3个、第4个正方形的面积.
解:∵点A的坐标为(1,0),点D的坐标为(0,2).
∴OA=1,OD=2,
在Rt△AOD中,AD=![]() ,
,
∴正方形ABCD的面积为:(![]() )2=5;
)2=5;
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,
∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°,
∴∠ADO=∠BAA1,
∵∠DOA=∠ABA1,
∴△DOA∽△ABA1,
∴![]() ,即
,即![]() ,
,
解得:A1B=![]() ,
,
∴A1C=A1B+BC=![]() ,
,
∴正方形A1B1C1C的面积为:(![]() )2=
)2=![]() ;
;
∵第1个正方形ABCD的面积为:5;
第2个正方形A1B1C1C的面积为:![]() =
=![]()
同理可得:第3个正方形A2B2C2C1的面积为:![]() =(
=(![]() )2×5;
)2×5;
∴第4个正方形A3B3C3C2的面积为:(![]() )3×5.
)3×5.
故答案为:5,(![]() )3×5.
)3×5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从1这点开始跳,则经过2019次跳后它所停在的点对应的数为( )
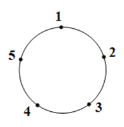
A. 1 B. 2 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△ABC中,∠ACB=90°,AC=BC.
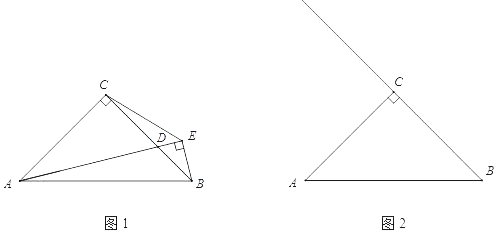
(1)如图1,点D是BC边上一点(不与点B,C重合),连接AD,过点B作BE⊥AD,交AD的延长线于点E,连接CE.若∠BAD=α,求∠DBE的大小(用含α的式子表示);
(2)如图2,点D在线段BC的延长线上时,连接AD,过点B作BE⊥AD,垂足E在线段AD上,连接CE.
①依题意补全图2;
②用等式表示线段EA,EB和EC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
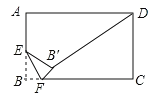
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将ΔEBF沿EF所在直线折叠得到ΔEB' F,连接B' D,则B' D的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
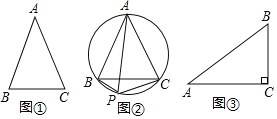
【题目】问题探究:
(1)已知:如图①,△ABC中请你用尺规在BC边上找一点D,使得点A到点BC的距离最短.
(2)托勒密(Ptolemy)定理指出,圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②,P是正△ABC外接圆的劣弧BC上任一点(不与B、C重合),请你根据托勒密(Ptolemy)定理证明:PA=PB+PC
问题解决:
(3)如图③,某学校有一块两直角边长分别为30m、60m的直角三角形的草坪,现准备在草坪内放置一对石凳及垃圾箱在点P处,使P到A、B、C三点的距离之和最小,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离(结果保留根号);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
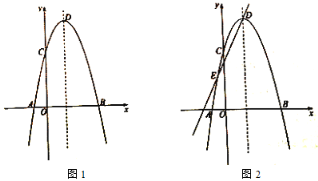
【题目】如图1,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线的顶点.
为抛物线的顶点.
(1)若![]() 点坐标为
点坐标为![]() ,求抛物线的解析式和点
,求抛物线的解析式和点![]() 的坐标;
的坐标;
(2)若点![]() 为抛物线对称轴上一点,且点
为抛物线对称轴上一点,且点![]() 的纵坐标为
的纵坐标为![]() ,点
,点![]() 为抛物线在
为抛物线在![]() 轴上方一点,若以
轴上方一点,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形时,求
为顶点的四边形为平行四边形时,求![]() 的值;
的值;
(3)直线![]() 与(1)中的抛物线交于点
与(1)中的抛物线交于点![]() 、
、![]() (如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为
(如图2),将(1)中的抛物线沿着该直线方向进行平移,平移后抛物线的顶点为![]() ,与直线的另一个交点为
,与直线的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,在平移的过程中,求
,在平移的过程中,求![]() 的长度;当
的长度;当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 经过
经过![]() 两点,交
两点,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
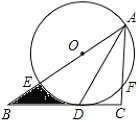
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径是
的半径是![]() ,
,![]() 是弧
是弧![]() 的中点,求阴影部分的面积(结果保留
的中点,求阴影部分的面积(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com