
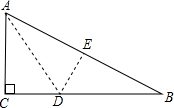
 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则AD=3$\sqrt{5}$cm.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则AD=3$\sqrt{5}$cm. 分析 根据翻折的性质可知:AC=AE=6,CD=DE,设CD=DE=x,在Rt△DEB中利用勾股定理解决.
解答 解: 在Rt△ABC中,∵AC=6,BC=8,
在Rt△ABC中,∵AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵△ADE是由△ACD翻折,
∴AC=AE=6,EB=AB-AE=10-6=4,
设CD=DE=x,
在Rt△DEB中,∵DE2+EB2=DB2,
∴x2+42=(8-x)2
∴x=3,
∴CD=3.
在Rt△ACD中,AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$.
故答案为3$\sqrt{5}$.
点评 本题考查翻折的性质、勾股定理,利用翻折不变性是解决问题的关键,学会转化的思想去思考问题.


科目:初中数学 来源: 题型:解答题
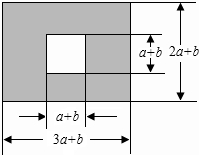 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形广场,规划部门将阴影部分进行绿化,中间边长为(a+b)米的正方形将修建一座雕塑,则:
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形广场,规划部门将阴影部分进行绿化,中间边长为(a+b)米的正方形将修建一座雕塑,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
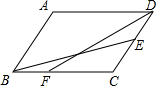 如图,在?ABCD中,AB:BC=2:3,点E、F分别在边CD、BC上,点E是边CD的中点,CF=2BF,∠A=120°,过点A分别作AP⊥BE、AQ⊥DF,垂足分别为P、Q,那么$\frac{AP}{AQ}$的值为$\frac{2\sqrt{39}}{13}$.
如图,在?ABCD中,AB:BC=2:3,点E、F分别在边CD、BC上,点E是边CD的中点,CF=2BF,∠A=120°,过点A分别作AP⊥BE、AQ⊥DF,垂足分别为P、Q,那么$\frac{AP}{AQ}$的值为$\frac{2\sqrt{39}}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a+\frac{7b}{10}$ | B. | $a+\frac{10b}{7}$ | C. | $b+\frac{7a}{10}$ | D. | $b+\frac{10a}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y3<y2 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y3<y1<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com