
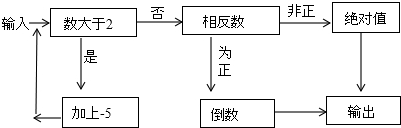
分析 (1)由-3<2结合相反数和倒数的定义即可得出输入-3时输出的数;由$\frac{9}{5}$<2结合相反数和倒数的定义即可得出输入$\frac{9}{5}$时输出的数;
(2)当输入0时可知输出0,当输入5的倍数时,根据运算即可得出输出为0,由此即可得出结论;
(3)根据有理数的转换即可得出输出的数非负,此题得解.
解答 解:(1)∵-3<2,-3的相反数为3,3的倒数为$\frac{1}{3}$,
∴输入-3时,输出的结果为$\frac{1}{3}$;
∵$\frac{9}{5}$<2,$\frac{9}{5}$的相反数为-$\frac{9}{5}$,-$\frac{9}{5}$的绝对值为$\frac{9}{5}$,
∴输入$\frac{9}{5}$时,输出的结果为$\frac{9}{5}$.
故答案为:$\frac{1}{3}$;$\frac{9}{5}$.
(2)当输入0时,0<2且0非正,
∴输出0;
当输入5的倍数时,输出0.
故答案为:0或5n(n为正整数);
(3)∵为正输出倒数,非正输出绝对值,
∴输出的数均为非负数.
故答案为:负.
点评 本题考查了有理数的混合运算,观察“有理数转换器”的转换找出运算规则是解题的关键.


科目:初中数学 来源: 题型:解答题
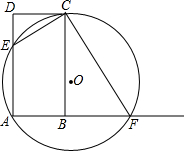 如图,在矩形ABCD中,AB=1,BC=2,点E是AD边上一动点(不与点A,D重合 ),过A、E、C三点的⊙O交AB延长线于点F,连接CE、CF.
如图,在矩形ABCD中,AB=1,BC=2,点E是AD边上一动点(不与点A,D重合 ),过A、E、C三点的⊙O交AB延长线于点F,连接CE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 70°和110° | B. | 80°和120° | C. | 40°和140° | D. | 100°和140° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 119 | C. | 120 | D. | 319 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
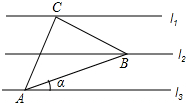 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{6}{17}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
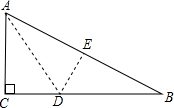 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则AD=3$\sqrt{5}$cm.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则AD=3$\sqrt{5}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com