练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】巴中市某楼盘准备以每平方米5000元的均价对外销售，由于有关部门关于房地产的新政策出台后，部分购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4050元的均价开盘销售，若两次下调的百分率相同，求平均每次下调的百分率．

    【答案】解：设平均每次下调的百分率为x，

    根据题意得：5000（1﹣x）2=4050，

    解得：x1=0.1=10%，x2=1.9（不合题意，舍去）．

    答：平均每次下调的百分率为10%


    【解析】设平均每次下调的百分率为x，根据调价前后的价格，即可得出关于x的一元二次方程，解之取小于1的正值即可得出答案.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，经过点A（0，﹣4）的抛物线y=x2+bx+c与x轴相交于点B（﹣1，0）和C，O为坐标原点．

    （1）求抛物线的解析式；

    （2）将抛物线y=x2+bx+c向上平移个单位长度，再向左平移m（m＞0）个单位长度，得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围；

    （3）将x轴下方的抛物线图象关于x轴对称，得到新的函数图象C，若直线y=x+k与图象C始终有3个交点，求满足条件的k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本小题满分8分）如图，四边形ABCD、DEFG都是正方形，连接AE、CG、AE与CG相交于点M，CG与AD相交于点N．

    求证：（1）AE=CG；

    （2）ANDN=CNMN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′OP=r2，则称点P′是点P关于⊙O的“反演点”．

    如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】铅笔每支m元，小明用10元钱买了n支铅笔后，还剩下元.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一坐标系中，一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C、D两点.点P是x轴上的一个动点.

    (1)求此抛物线的解析式；

    (2)当PA+PB的值最小时，求点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根，下列结论：

    ①b2﹣4ac＜0；②abc＞0；③a﹣b+c＜0；④m＞﹣2，

    其中，正确的个数有（　　）

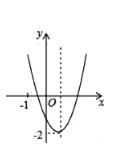
    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a＋b＝5，ab＝3，则a2＋b2的值为（ ）

    A. 19B. 25C. 8D. 6

    查看答案和解析>>

    同步练习册答案