
分析 (1)根据题意可以分别表示出第3天和第5天的植树量;
(2)根据题意可以列出相应的式子,求出开始时的人数,从而可以解答本题.
解答 解:(1)由题意可得,
第三天有(m-5)个人,每人植树(n+5)棵,
∴第三天共植树为:(m-5)(n+5)=(mn+5m-5n-25)棵,
第五天有(m+5)个人,每人植树(n-5)棵,
∴第五天共植树为:(m+5)(n-5)=(mn-5m+5n-25)棵,
故答案为:(mn+5m-5n-25),(mn-5m+5n-25);
(2)设第4天m人植树,每人植树n棵,
则第一天植树:(m-15)(n+15),
第二天植树:(m-10)(n+10),
第三天植树:(m-5)(n+5),
第四天植树:mn,
第五天植树:(m+5)(n-5),
第六天植树:(m+10)(n-10),
第七天植树:(m+15)(n-15),
∴(m-15)(n+15)+(m-10)(n+10)+(m-5)(n+5)+mn+(m+5)(n-5)+(m+10)(n-10)+(m+15)(n-15)=9947,
化简,得
mn=1521,
∵m、n均为正整数,且每天都有人植树,
∴m=39,n=39,
由上可得,第四天是mn=1521棵,
其它每天植树为(39+a)(39-a)=392-a2,(a=5,10,15)
∴植树最多的是第四天,此时植树1521棵,
当a=15时,植树最少,这天是第一天或第七天,
39+a=64,39-a=24,
即七天中植树最多的那天共植了1521棵树,植树最少的那天,有64人或24人在植树.
点评 本题考查整式的混合运算、非负数的性质,解答此类问题的关键是明确题意,找出所求问题需要的条件,注意理论联系实际.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
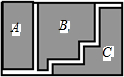 如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.
如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3级 | B. | 4级 | C. | 5级 | D. | 6级 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000 cm2 | B. | 100m2 | C. | 10m2 | D. | 100000cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com