
【题目】如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20,求∠OFE的度数.
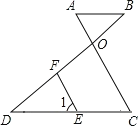
【答案】(1)证明见解析(2)100°
【解析】分析:(1)由AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由已知角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由EF与OC平行,利用两直线平行同旁内角互补得到一对角互补,利用等角的补角相等得到∠BOC+∠DFE=180°,结合∠BOC+∠DFE=180°,求出∠OFE的度数即可.
详解:(1)∵AB∥DC,∴∠C=∠A.∵∠1=∠A,∴∠1=∠C,∴FE∥OC;
(2∵FE∥OC,∴∠FOC+∠OFE=180°.∵∠FOC+∠BOC=180°,∠DFE+∠OFE=180°,∴∠BOC+∠DFE=180°.∵∠BOC﹣∠DFE=20°,∴∠BOC+∠DFE=180°,解得:∠DFE=80°,∴∠OFE=100°.


科目:初中数学 来源: 题型:
【题目】一种细胞的直径约为0.000067米,将0.000067用科学记数法表示为( )
A.6.7×105B.6.7×106C.6.7×10-5D.6.7×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
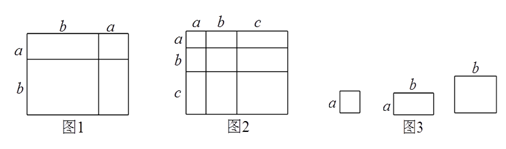
【题目】【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图![]() 可以得到
可以得到![]() ,基于此,请解答下列问题:
,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,![]() = .
= .
(3) 小明同学用图 中x 张边长为a 的正方形, y张边长为b 的正方形,z 张宽、长分别为 a、b 的长方形纸片拼出一个面积为 (2a+b)(a+2b)长方形,则x+y+z=
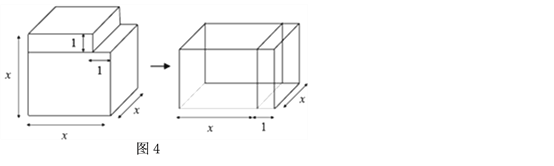
【知识迁移】(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为![]() 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影院里,我们常用“几行几列”来描述一张票对应的位置,现引入这样的思想,用如图的两个互相垂直的数轴来描述这样的点位,只不过这个点位信息会有负数甚至0哦。图中正方形网格的边长均为1个单位长。比如图中的点P,我们用(横向对应数值,竖向对应数值)来定义其点位信息,其点位记作(4,-2);再如△ABC,其顶点都在格点上,其中A记作(4,4)、B记作(1,2)、C记作(3,2).请解答下列问题:
(1)将△ABC向下平移5个单位长,再向左平移2个单位长,画出两次平移后得到的△A1B1C1;
(2)给出A1、B1、C1的点位:A1(_____),___)、B1(_____),___)、C1(_____),___);
(3)点E、F点位分别为E(-4,3)、F(0,-3),则线段EF与线段AB的关系为______________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会求![]() 的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]()
![]()
![]()
(1)由上面的规律我们可以大胆猜想,得到![]() =________
=________
利用上面的结论,求
(2)![]() 的值;
的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
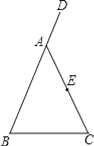
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com