
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=8,AD=14,点E、F、G分别在BC、AB、AD上,且BE=3,BF=2,以EF、FG为邻边作□EFGH,设AG=![]() .
.
(1)直接写出点H到AD的距离;
(2)若点H落在梯形ABCD内或其边上,求△HGD面积的最大值与最小值;
(3)当![]() 为何值时,△EHC是等腰三角形.
为何值时,△EHC是等腰三角形.
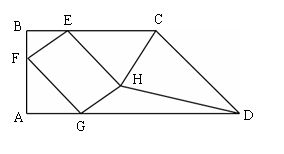
解:(1)点H到AD的距离为2;
(2)∵△HGD中GD边上的高为2
①当△HDG面积取得取大值时,底边GD最大,
此时点G与点A重合,如图1,
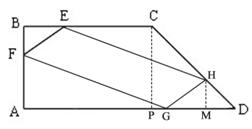
 ∴GD=AD=14 ∴S△HGD的最大值是14.
∴GD=AD=14 ∴S△HGD的最大值是14.
图1 图2
②当△HGD面积取得最小值时,底边GD最小.
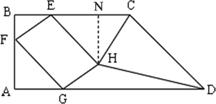
此时点H在CD边上,如图2,
过C作CP⊥AD于P,DP=AD-AP=AD-BC=6
又∵CP=AB=6 ∴∠D=45°
过点H作HM⊥AD于M,则MD=MH=2
显然△HMG≌△FBE ∴GM=BE=3
∴GD=GM+MD=5 ∴S△HGD的最小值是5
、
(3)过H作HN⊥BC于N,如图3显然Rt△FAG≌Rt△HNE
∵EC=BC-BE=5 HN=FA=AB-FB=4,EN=AG=x
∵△EHC是等腰三角形
①当EH=EC时,EH=5,HN=4 ∴EN=3 即x=3
②当HC=EC时,HC=5,HN=4 ∴NC=3
EN=EC-NC=2 即x=2
③当EH=HC时,EN=NC=![]() EC=2.5
EC=2.5
综上所述,当x=2或2.5或3时,
△EHC是等腰三角形


科目:初中数学 来源: 题型:
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).查看答案和解析>>
科目:初中数学 来源: 题型:
 (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
 BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com