
分析 先本方程化为一般式得到2a2x2+2ax+1-a2=0,利用两根之积可判断两根异号,则x1<0<x2,设y=2a2x2+2ax+1-a2,利用对称轴方程可判断对称轴的位置如图所示,然后分别计算出自变量为-1和1所对应的函数值即可判断-1<x1<0<x2<1.
解答 证明:方程化为一般式得2a2x2+2ax+1-a2=0,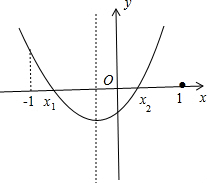
∵x1•x2=$\frac{1-{a}^{2}}{2{a}^{2}}$,
而a>1,
∴x1•x2<0,
∵x1<0<x2,
设y=2a2x2+2ax+1-a2,
抛物线的对称轴为直线x=-$\frac{2a}{2•{2a}^{2}}$=-$\frac{1}{2a}$,
∴-1<-$\frac{1}{2a}$<0,如图,
当x=-1时,y=a2-2a+1=(a-1)2>0,
当x=1时,y=a2+2a+1=(a+1)2>0,
∴-1<x1<0<x2<1.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了数形结合思想的运用.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
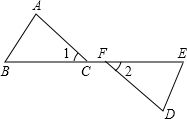 如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )
如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )| A. | AB=DE | B. | ∠B=∠F | C. | BF=CE | D. | ∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
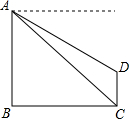 小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°.
小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | (n-1)枚棋子 | B. | n枚棋子 | C. | (n+1)枚棋子 | D. | (3n-2)枚棋子 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com