
分析 (1)利用直接开平方法解方程;
(2)先利用代入法消去y得到关于x的一元二次方程x2-3x+2=0,利用因式分解法求出x,然后计算出对应的y的值即可得到方程组的解;
(3)先去分母,把方程转化为3x2+7x+2=0,利用因式分解法求出x,然后进行检验确定原方程的解;
(4)利用换元法解方程:设$\frac{{x}^{2}+1}{x+2}$=t,原方程化为t+$\frac{2}{t}$=3,解此分式方程得到t1=1,t2=2,然后分别解$\frac{{x}^{2}+1}{x+2}$=1和$\frac{{x}^{2}+1}{x+2}$=2,最后进行检验确定原方程的解.
解答 解:(1)2x+1=±(x-1)
解得x1=-2,x2=0;
(2)$\left\{\begin{array}{l}{x+y=3①}\\{(x+y)^{2}+2(x+y)-2xy=11②}\end{array}\right.$,
把①代入②得:9+6-2xy=11,
即2xy=4,即xy=2③,
由①得:y=-x+3,代入③得:x(-x+3)=2,
整理得:x2-3x+2=0,即(x-1)(x-2)=0,
解得x=1或x=2,
把x=1代入①得:y=2;
把x=2代入①得:y=1,
所以方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(3)去分母得:-2x(x+2)-x2+4=4+3(x+2),
去括号得:-2x2-4x-x2+4=4+3x+6,即3x2+7x+2=0,
(3x+1)(x+2)=0,
所以x1=-$\frac{1}{3}$,x2=-2,
经经验x=-$\frac{1}{3}$是原方程的解,
所以原方程的解为x=-$\frac{1}{3}$;
(4)设$\frac{{x}^{2}+1}{x+2}$=t,
则原方程化为t+$\frac{2}{t}$=3,
去分母得t2-3t+2=0,解得t1=1,t2=2,
当t=1时,$\frac{{x}^{2}+1}{x+2}$=1,解得x1=$\sqrt{2}$,x2=-$\sqrt{2}$,
当t=2时,$\frac{{x}^{2}+1}{x+2}$=2,解得x1=$\frac{1+\sqrt{17}}{2}$,x2=$\frac{1-\sqrt{17}}{2}$,
经经验原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$,x3=$\frac{1+\sqrt{17}}{2}$,x4=$\frac{1-\sqrt{17}}{2}$.
所以原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$,x3=$\frac{1+\sqrt{17}}{2}$,x4=$\frac{1-\sqrt{17}}{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了解分式方程.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,a,b,c是数轴上三个点A、B、C所对应的实数,|a|<|c|,试化简:($\sqrt{c}$)2+|a-b|+$\root{3}{(a+b)^{3}}$-|a+c|
如图,a,b,c是数轴上三个点A、B、C所对应的实数,|a|<|c|,试化简:($\sqrt{c}$)2+|a-b|+$\root{3}{(a+b)^{3}}$-|a+c|查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
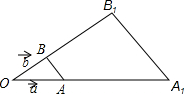 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com