
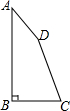
 如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.
如图,四边形ABCD中,AB⊥BC,∠A+∠B=160°,∠D=4∠C,求四边形ABCD各内角的度数.  同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
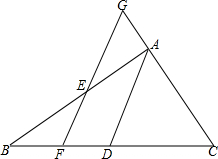 如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F
如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
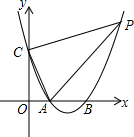 如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
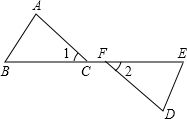 如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )
如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是( )| A. | AB=DE | B. | ∠B=∠F | C. | BF=CE | D. | ∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.
如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.| A. | 15.6 | B. | 6.4 | C. | 3.4 | D. | 3.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com