
 如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由.
如图,在△ABC中,AB=AC,∠C=2∠A,BD平分∠ABC.请找出图中其他的等腰三角形,并选择其中的一个说明理由. 分析 由在△ABC中,AB=AC,∠C=2∠A,可求得5∠A=180°,继而求得∠A,∠ABC与∠C的度数,然后由BD平分∠ABC,易得∠A=∠ABD,∠C=∠BDC,则可证得结论.
解答 解:△ABD、△BCD.
理由:∵在△ABC中,AB=AC,∠C=2∠A,
∴∠ABC=∠C=2∠A,
∵∠A+∠ABC+∠C=180°,
∴∠A+2∠A+2∠A=180°,
解得:∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,
∴∠A=∠ABD=36°,∠BDC=∠C=72°,
∴△ABD与△BCD是等腰三角形.
点评 此题考查了等腰三角形的性质与判定.注意由已知条件求得各角的度数是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
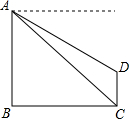 小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°.
小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.
如图,为了测量校园水平地面上一棵树的高度,数学兴趣小组做了如下的探索:把一面很小的镜子水平放置在离树底(B)7.8米的点E处,然后观察者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为( )米.| A. | 15.6 | B. | 6.4 | C. | 3.4 | D. | 3.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | (n-1)枚棋子 | B. | n枚棋子 | C. | (n+1)枚棋子 | D. | (3n-2)枚棋子 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com