
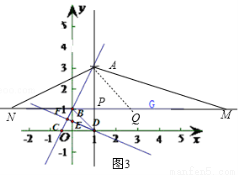
(10分)直线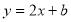 经过点A(1,3),与y轴交于点B,与x轴交于点C.
经过点A(1,3),与y轴交于点B,与x轴交于点C.
(1)求直线AB的解析式;
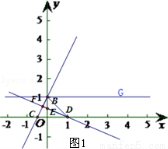
(2)将直线AB绕点O顺时针旋转900,与x轴交于点D,与y轴交于点E,与直线AB交于点F,求△BDF的面积;
(3)过B点作x轴的平行线BG,点M在直线BG上,且到点(1,1)的距离为6,设点N在直线BG上,请你直接写出使得∠AMB+∠ANB = 450的点N的坐标.
(1)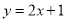 ;(2)
;(2)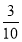 ;(3)N(5,1)或N(-3,1).
;(3)N(5,1)或N(-3,1).
【解析】
试题分析:(1)把A的坐标代入即可求出结论;
(2)根据旋转的性质就可以求出D、E的坐标,由勾股定理就可以求出BD,DE、DF的值根据三角形面积公式就可以求出结论;
(3)根据题意画出图形,分情况讨论运用相似三角形的性质就可以求出结论.
试题解析:(1)∵直线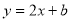 经过点A(1,3),∴
经过点A(1,3),∴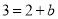 ,∴
,∴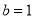 ,∴直线AB为:
,∴直线AB为: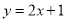 ;
;
(2)令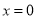 ,则
,则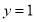 ,令
,令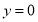 ,则
,则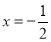 ,∴B(0,1),C(
,∴B(0,1),C(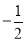 ,0),将直线AB绕O点顺时针旋转900,设DE与BC交于点F,∴D(1,0),E(0,
,0),将直线AB绕O点顺时针旋转900,设DE与BC交于点F,∴D(1,0),E(0,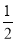 ),∠CFD=90°,∴OB=OD=1,OC=
),∠CFD=90°,∴OB=OD=1,OC=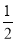 ,∴CD=
,∴CD=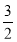 ,
,
在Rt△BOC中,由勾股定理,得CB=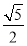 ,BD=
,BD=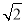 .∵CD•OB=CB•DF,∴DF=
.∵CD•OB=CB•DF,∴DF=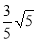 ,∴由勾股定理,得BF=
,∴由勾股定理,得BF=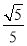 ,∴
,∴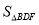 =
=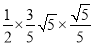 =
=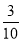 ;
;
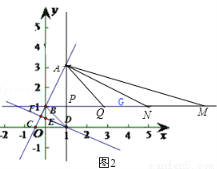
(3)如图2,在BG上取一点Q,使AP=QP,∴∠AQP=45°,∴∠ANB+∠QAN=∠QAM+∠AMB=45°,∵∠AMB+∠ANB=45°,∴∠ANB=∠QAM,∴△AQN∽△MQA,∴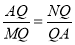 ,∵AD=3,OD=1,∴AP=QP=2,∴QM=4,AQ=
,∵AD=3,OD=1,∴AP=QP=2,∴QM=4,AQ=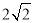 ,∵MP=6,∴MQ=4.∴
,∵MP=6,∴MQ=4.∴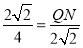 ,∴QN=2,∴BN=5,∴N(5,1);
,∴QN=2,∴BN=5,∴N(5,1);
如图3,在BG上取一点Q,使AP=QP,∴∠AQP=45°,∴∠ANB+∠AMB=∠QAM+∠AMB=45°,∴∠ANB=∠QAM,∴△AQM∽△NAM,∴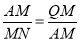 .∵AD=3,OD=1,∴AP=QP=2,∴QM=4,BM=7,AQ=
.∵AD=3,OD=1,∴AP=QP=2,∴QM=4,BM=7,AQ=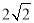 ,∵MP=6,∴MQ=4.AM=
,∵MP=6,∴MQ=4.AM=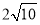 ,∴
,∴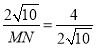 ,∴MN=10,∴BN=3.∴N(﹣3,1);∴N(﹣3,1)或(5,1).
,∴MN=10,∴BN=3.∴N(﹣3,1);∴N(﹣3,1)或(5,1).
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
(本小题满分10分)如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.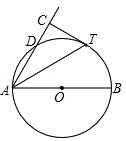
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,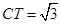 ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
已知点P(1,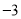 )在反比例函数
)在反比例函数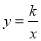 (
(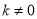 )的图象上,则k的值是( )
)的图象上,则k的值是( )
A.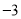 B.3 C.
B.3 C.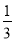 D.
D.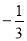
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省伊春市九年级11月月考数学试卷(解析版) 题型:解答题
(8分)二次函数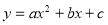
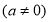 的图象经过点A(3,0),B(2,-3),并且以
的图象经过点A(3,0),B(2,-3),并且以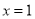 为对称轴.
为对称轴.
(1)求此函数的解析式;
(2)在对称轴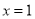 上是否存在一点P,使PA=PB,若存在,求出P点的坐标,若不存在,说明理由.
上是否存在一点P,使PA=PB,若存在,求出P点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(11分)某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:

(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省漯河市九年级上期末模拟数学试卷(解析版) 题型:选择题
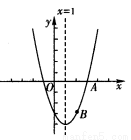
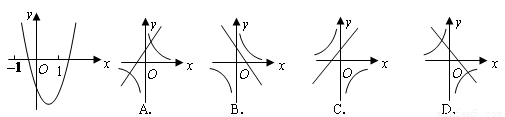
二次函数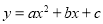 的图象如图所示,则一次函数
的图象如图所示,则一次函数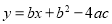 与反比例函数
与反比例函数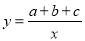 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com